题目内容
如图,在平面直角坐标系中,点A(-4,4),点B(-4,0),将△ABO绕原点O按顺时针方向旋转135°得到△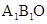 。回答下列问题:(直接写结果)
。回答下列问题:(直接写结果)
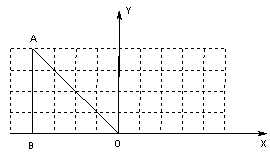
(1)∠AOB= °;
°;
(2)顶点A从开始到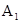 经过的路径长为
经过的路径长为  ;
;
(3)点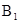 的坐标为
的坐标为
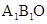 。回答下列问题:(直接写结果)
。回答下列问题:(直接写结果)
(1)∠AOB=
 °;
°;(2)顶点A从开始到
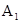 经过的路径长为
经过的路径长为  ;
;(3)点
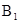 的坐标为
的坐标为
解:(1)450;(2)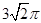 ;(3)(2
;(3)(2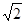 ,2
,2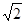 )
)
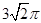 ;(3)(2
;(3)(2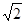 ,2
,2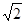 )
)分析:
(1)先求出∠AOB=45°,再根据旋转变换只改变图形的位置不改变图形的形状与大小解答;
(2)根据等腰直角三角形的直角边等于斜边的
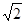 /2计算即可得解;
/2计算即可得解;(3)利用勾股定理列式求出OA的长,再根据弧长公式进行计算即可得解。
解答:
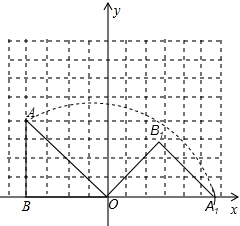
(1)∵点A(-4,4),点B(-4,0),
∴△AOB是等腰直角三角形,∠AOB=45°,
∵△ABO绕原点O按顺时针方向旋转135°得到△A1B1O,
∴∠A1OB1=∠AOB=45°;
(2)由图可知,OB1=OB=4,4×
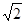 /2=2
/2=2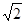
∴点B1的坐标为(2
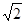 ,2
,2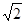 )
)(3)根据勾股定理,OA2=42+42
∴OA=4
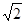
点A从开始到A1经过的路径长=135?π?4
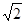 /180=
/180=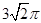 。
。点评:本题考查了利用旋转变换作图,弧长的计算,以及等腰直角三角形的性质,熟练掌握网格结构,准确找出对应点的位置并熟记各性质与弧长公式是解题的关键。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
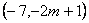 在第三象限,则m的取值范围是
在第三象限,则m的取值范围是
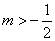
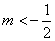
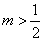
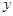 轴对称,则点N的坐标为( ).
轴对称,则点N的坐标为( ).

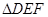 ,
, 是沿
是沿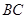 方向平移后的图形,试判断
方向平移后的图形,试判断 与
与 的面积关系是___________
的面积关系是___________