题目内容
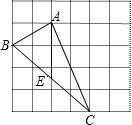 如图,在由边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,E为BC中点,请按要求完成下列各题:
如图,在由边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,E为BC中点,请按要求完成下列各题:(1)画AD∥BC(D为格点),连接CD;
(2)通过计算说明△ABC是直角三角形;
(3)在△ACB中,tan∠CAE=
分析:(1)根据题意,画出AD∥BC(D为格点),连接CD;
(2)在网格中利用直角三角形,先求BC2,AB2,AC2的值,再比较列出等式,判断直角三角形;
(3)把问题转化到Rt△ACF,Rt△ADC中,利用三角函数的定义解题.
(2)在网格中利用直角三角形,先求BC2,AB2,AC2的值,再比较列出等式,判断直角三角形;
(3)把问题转化到Rt△ACF,Rt△ADC中,利用三角函数的定义解题.
解答:解:(1)图象如图所示;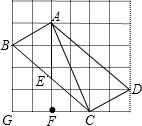
(2)由图象可知AB2=12+22=5,AC2=22+42=20,BC2=32+42=25,
∴BC2=AB2+AC2,△ABC是直角三角形;
(3)∵BG∥AF,F为CG的中点,
∴BC的中点E在线段AF上,
由图象可知CD=
,AD=5,
∴tan∠CAE=tan∠CAF=
=
,sin∠CAD=
=
.
故答案为:
,
.

(2)由图象可知AB2=12+22=5,AC2=22+42=20,BC2=32+42=25,
∴BC2=AB2+AC2,△ABC是直角三角形;
(3)∵BG∥AF,F为CG的中点,
∴BC的中点E在线段AF上,
由图象可知CD=
| 5 |
∴tan∠CAE=tan∠CAF=
| 2 |
| 4 |
| 1 |
| 2 |
| CD |
| AD |
| ||
| 5 |
故答案为:
| 1 |
| 2 |
| ||
| 5 |
点评:本题考查了勾股定理及其逆定理的运用,锐角三角函数的定义,关键是运用网格表示线段的长度.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案
相关题目
 24、如图,在由边长为1的小正方形组成的方格纸中,有两个全等的三角形,即△A1B1C1和△A2B2C2.
24、如图,在由边长为1的小正方形组成的方格纸中,有两个全等的三角形,即△A1B1C1和△A2B2C2.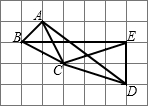 已知:如图,在由边长为1的小正方形组成的网格中,点A、B、C、D、E都在小正方形的顶点上,求tan∠ADC的值.
已知:如图,在由边长为1的小正方形组成的网格中,点A、B、C、D、E都在小正方形的顶点上,求tan∠ADC的值.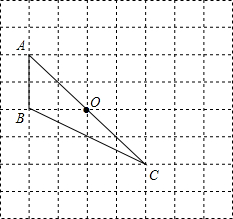 (2012•阜新)如图,在由边长为1的小正方形组成的网格中,三角形ABC的顶点均落在格点上.
(2012•阜新)如图,在由边长为1的小正方形组成的网格中,三角形ABC的顶点均落在格点上. 如图,在由边长为1的小正方形组成的方格纸中,有两个全等的三角形,即△A1B1C1和△A2B2C2.请你指出在方格纸内如何运用平移、旋转变换,将△A1B1C1重合到△A2B2C2上.
如图,在由边长为1的小正方形组成的方格纸中,有两个全等的三角形,即△A1B1C1和△A2B2C2.请你指出在方格纸内如何运用平移、旋转变换,将△A1B1C1重合到△A2B2C2上.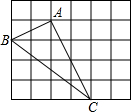 如图,在由边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题:
如图,在由边长为1的小正方形组成的网格中,△ABC的三个顶点均在格点上,请按要求完成下列各题: