题目内容
(2009•怀化)如图,已知二次函数y=(x+m)2+k-m2的图象与x轴相交于两个不同的点A(x1,0)、B(x2,0),与y轴的交点为C.设△ABC的外接圆的圆心为点P.(1)求⊙P与y轴的另一个交点D的坐标;
(2)如果AB恰好为⊙P的直径,且△ABC的面积等于
 ,求m和k的值.
,求m和k的值.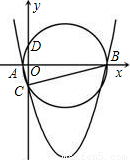
【答案】分析:(1)令x=0,代入抛物线解析式,即求得点C的坐标.由求根公式求得点A、B的横坐标,得到点A、B的横坐标的和与积,由相交弦定理求得OD的值,从而得到点D的坐标.
(2)当AB又恰好为⊙P的直径,由垂径定理知,点C与点D关于x轴对称,故得到点C的坐标及k的值.根据一元二次方程的根与系数的关系式表示出AB线段的长,由三角形的面积公式表示出△ABC的面积,可求得m的值.
解答: 解:(1)易求得点C的坐标为(0,k)
解:(1)易求得点C的坐标为(0,k)
由题设可知x1,x2是方程(x+m)2+k-m2=0即x2+2mx+k=0的两根,
所以x1,2=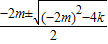 ,
,
所x1+x2=-2m,x1•x2=k(1分)
如图,∵⊙P与y轴的另一个交点为D,由于AB、CD是⊙P的两条相交弦,设它们的交点为点O,连接DB,
∴△AOC∽△DOB,则OD= (2分)
(2分)
由题意知点C在y轴的负半轴上,从而点D在y轴的正半轴上,
所以点D的坐标为(0,1)(3分)
(2)∵AB⊥CD,AB又恰好为⊙P的直径,则C、D关于点O对称,
所以点C的坐标为(0,-1),
即k=-1(4分)
又AB=|x2-x1|= =
=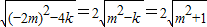 ,
,
所以S△ABC= AB×OC=
AB×OC= ×2
×2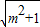 ×1=
×1=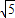 ,
,
解得m=±2.(正值舍去)(6分)
∴k=-1,m=-2.
点评:本题考查了一元二次方程的求根公式,根与系数的关系,相交弦定理,垂径定理,三角形的面积公式.如何表示OD及AB的长是本题中解题的关键.
(2)当AB又恰好为⊙P的直径,由垂径定理知,点C与点D关于x轴对称,故得到点C的坐标及k的值.根据一元二次方程的根与系数的关系式表示出AB线段的长,由三角形的面积公式表示出△ABC的面积,可求得m的值.
解答:
 解:(1)易求得点C的坐标为(0,k)
解:(1)易求得点C的坐标为(0,k)由题设可知x1,x2是方程(x+m)2+k-m2=0即x2+2mx+k=0的两根,
所以x1,2=
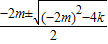 ,
,所x1+x2=-2m,x1•x2=k(1分)
如图,∵⊙P与y轴的另一个交点为D,由于AB、CD是⊙P的两条相交弦,设它们的交点为点O,连接DB,
∴△AOC∽△DOB,则OD=
 (2分)
(2分)由题意知点C在y轴的负半轴上,从而点D在y轴的正半轴上,
所以点D的坐标为(0,1)(3分)
(2)∵AB⊥CD,AB又恰好为⊙P的直径,则C、D关于点O对称,
所以点C的坐标为(0,-1),
即k=-1(4分)
又AB=|x2-x1|=
 =
=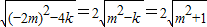 ,
,所以S△ABC=
 AB×OC=
AB×OC= ×2
×2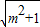 ×1=
×1=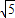 ,
,解得m=±2.(正值舍去)(6分)
∴k=-1,m=-2.
点评:本题考查了一元二次方程的求根公式,根与系数的关系,相交弦定理,垂径定理,三角形的面积公式.如何表示OD及AB的长是本题中解题的关键.

练习册系列答案
相关题目
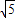 ,求m和k的值.
,求m和k的值.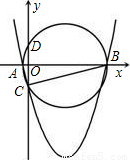
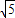 ,求m和k的值.
,求m和k的值.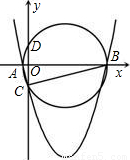
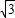 m到B地,再从B地向正南方向走200m到C地,此时小明离A地 m.
m到B地,再从B地向正南方向走200m到C地,此时小明离A地 m.
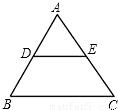 (2009•怀化)如图,D、E分别是AB、AC的中点,则S△ADE:S△ABC=( )
(2009•怀化)如图,D、E分别是AB、AC的中点,则S△ADE:S△ABC=( )