题目内容
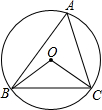 如图,∠A是⊙O的圆周角,∠A=60°,则∠OBC的度数为________度.
如图,∠A是⊙O的圆周角,∠A=60°,则∠OBC的度数为________度.
30
分析:根据圆周角定理求出∠BOC=2∠A=120°,根据等腰三角形性质求出∠OBC=∠OCB,在△BOC中,根据三角形的内角和定理求出即可.
解答:∵弧BC对的圆心角是∠BOC,对的圆周角是∠A,∠A=60°,
∴∠BOC=2∠A=120°,
∵OB=OC,
∴∠OBC=∠OCB,
∵∠OBC+∠OCB+∠BOC=180°,
∴∠OBC=30°,
故答案为:30.
点评:本题考查了等腰三角形的性质,三角形的内角和定理,圆周角定理的应用,解此题的关键是求出∠BOC的度数,题目比较典型,难度不大.
分析:根据圆周角定理求出∠BOC=2∠A=120°,根据等腰三角形性质求出∠OBC=∠OCB,在△BOC中,根据三角形的内角和定理求出即可.
解答:∵弧BC对的圆心角是∠BOC,对的圆周角是∠A,∠A=60°,
∴∠BOC=2∠A=120°,
∵OB=OC,
∴∠OBC=∠OCB,
∵∠OBC+∠OCB+∠BOC=180°,
∴∠OBC=30°,
故答案为:30.
点评:本题考查了等腰三角形的性质,三角形的内角和定理,圆周角定理的应用,解此题的关键是求出∠BOC的度数,题目比较典型,难度不大.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
 (1997•上海)如图,半径是5厘米的圆中,8厘米长的弦的弦心距是
(1997•上海)如图,半径是5厘米的圆中,8厘米长的弦的弦心距是
 如图,半径是5厘米的圆中,8厘米长的弦的弦心距是________厘米.
如图,半径是5厘米的圆中,8厘米长的弦的弦心距是________厘米.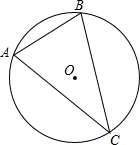 如图,⊙O是△ABC的________圆,△ABC是⊙O的________三角形.
如图,⊙O是△ABC的________圆,△ABC是⊙O的________三角形. 如图,半径是5厘米的圆中,8厘米长的弦的弦心距是 厘米.
如图,半径是5厘米的圆中,8厘米长的弦的弦心距是 厘米.