题目内容
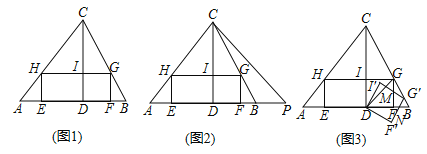
【题目】如图1．在△ABC中，矩形EFGH的一边EF在AB上，顶点G、H分别在BC、AC上，CD是边AB上的高，CD交GH于点I．若CI＝4，HI＝3，AD
．矩形DFGI恰好为正方形．
（1）求正方形DFGI的边长；
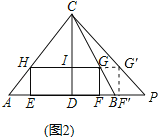
（2）如图2，延长AB至P．使得AC＝CP，将矩形EFGH沿BP的方向向右平移，当点G刚好落在CP上时，试判断移动后的矩形与△CBP重叠部分的形状是三角形还是四边形，为什么？
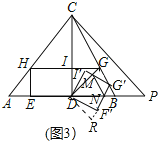
（3）如图3，连接DG，将正方形DFGI绕点D顺时针旋转一定的角度得到正方形DF′G′I′，正方形DF′G′I′分别与线段DG、DB相交于点M、N，求△MNG′的周长．
【答案】（1）2；（2）三角形；（3）4．
【解析】
(1)由HI∥AD，得到
，求出AD即可解决问题；
(2)如图2中，设点G落在PC时对应的点为G′，点F的对应的点为F′．求出IG′和BD的长比较即可判定；
(3)如图3中，如图将△DMI′绕点D逆时针旋转90°得到△DF′R，此时N、F′、R共线．想办法证明MN=MI′+NF′，即可解决问题.
(1)∵HI∥AD，
∴，
∴
，
∴AD＝6，
∴ID＝CD﹣CI＝2，∴正方形的边长为2；
(2)三角形，理由如下：
如图2中，设点G落在PC时对应的点为G′，点F的对应的点为F′．
∵CA＝CP，CD⊥PA，∴∠ACD＝∠PCD，∠A＝∠P，
∵HG′∥PA，
∴∠CHG′＝∠A，∠CG′H＝∠P，
∴∠CHG′＝∠CG′H，∴CH＝CG′，
∴IH＝IG′＝DF′＝3，
∵IG∥DB，∴
，
∴
，∴DB＝3，
∴DB＝DF′＝3，∴点B与点F′重合，
∴移动后的矩形与△CBP重叠部分是△BGG′，
∴移动后的矩形与△CBP重叠部分的形状是三角形；
(3)如图3中，如图将△DMI′绕点D逆时针旋转90°得到△DF′R，此时N、F′、R共线．
∵∠MDN＝∠NDF+∠MDI′＝∠NDF′+∠DF′R＝∠NDR＝45°，
∵DN＝DN，DM＝DR，
∴△NDM≌△NDR，
∴MN＝NR＝NF′+RF′＝NF′+MI′，
∴△MNG′的周长＝MN+MG′+NG′＝MG′+MI′+NG′+F′R＝2I′G′＝4．
