题目内容
【题目】如图1,在△ABC中,AB=AC=2,∠A=90°,将一块与△ABC全等的三角板的直角顶点放在点C上,一直角边与BC重叠.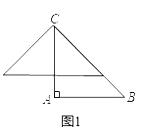
(1)操作1:固定△ABC,将三角板沿C→B方向平移,使其直角顶点落在BC的中点M,如图2所示,探究:三角板沿C→B方向平移的距离为;
(2)操作2:在(1)的情况下,将三角板BC的中点M顺时针方向旋转角度a(0°<a<90°),如图3所示,探究:设三角形板两直角边分别与AB、AC交于点P、Q,观察四边形MPAQ形状的变化,问:四边形MPAQ的面积S是否改变,若不变,求其面积;若改变,试说明理由;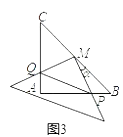
(3)在(2)的情形下,连PQ,则当△MPQ的面积等于四边形MPAQ的面积的一半时,四边形MPAQ的形状为 , 此时BP= .
【答案】
(1)![]()
(2)
答:四边形MPAQ的面积S不变.
解法1:连接AM,
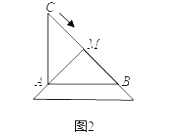

∵AB=AC=2,∠A=90°,
∴S△ABC= ![]() ABAC=
ABAC= ![]() ×2×2=2
×2×2=2
又由(1)知,点M是BC中点
∴∠CAM=∠BAM=∠B=45°,AM⊥BC,
∴AM=BM,∠BMP+∠PMA=90°
∴S△ABM= ![]() S△ABC=1
S△ABC=1
又∠AMQ+∠PMA=90°
∴∠AMQ=∠BMP
∴△AMQ≌△BMP
∴S四边形MPAQ=S△ABM=1,
解法2:如图3,作MD⊥AC于D,作ME⊥AB于E,
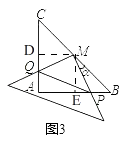
∵AB=AC=2,∠A=90°
∴∠B=∠C=45°,四边形ADME是矩形,
S△ABC= ![]() ABAC=
ABAC= ![]() ×2×2=2
×2×2=2
又∵点M是BC中点
∴Rt△CMD≌Rt△BME
∴四边形ADME是正方形,易求S正方形ADME= ![]() S△ABC=1
S△ABC=1
∴MD=ME,∠DMQ+∠QME=90°,
又∠EMP+∠QME=90°
∴∠DMQ=∠EMP
∴△DMQ≌△EMP
∴S四边形MPAQ=S正方形ADME=1,
(3)正方形;1
【解析】(1.)解:(1)BC= ![]() =2
=2 ![]() ,
,
∴CM= ![]() BC=
BC= ![]() 故三角板沿C→B方向平移的距离为:
故三角板沿C→B方向平移的距离为: ![]() ;
;
所以答案是: ![]() ;
;
(3.)设AQ=PB=x,AP=2﹣x,
S△MPQ=S四边形MAPQ﹣S△APQ=1﹣ ![]() AQAP=1﹣
AQAP=1﹣ ![]() x(2﹣x)=
x(2﹣x)= ![]() x2﹣x+1=
x2﹣x+1= ![]()
解得,x=1.
∴PB=1,
∴AQ=PB=AP=1,
∴点P是AB的中点,
∵M是BC中点,
∴PM∥AQ,
∴∠MPA=90°,
∵∠PAQ=∠PMQ=90°,
∴四边形MPAQ是矩形,
∵AQ=AP,
∴矩形MPAQ是正方形,
所以答案是:正方形,1.
【考点精析】解答此题的关键在于理解三角形的面积的相关知识,掌握三角形的面积=1/2×底×高,以及对相似三角形的性质的理解,了解对应角相等,对应边成比例的两个三角形叫做相似三角形.

【题目】光明中学八年级甲、乙、丙三个班中,每班的学生人数都为40名,某次数学考试的成绩统计如图:(每组分数含最小值,不含最大值)
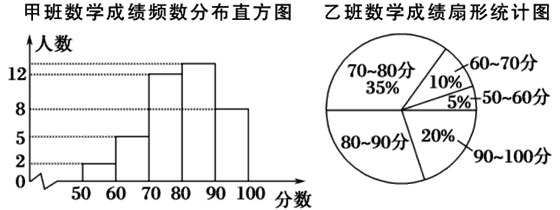
丙班数学成绩频数统计表
分数 | 50~60 | 60~70 | 70~80 | 80~90 | 90~100 |
人数 | 1 | 4 | 15 | 11 | 9 |
根据上图及统计表提供的信息,则80~90分这一组人数最多的班是________