��Ŀ����
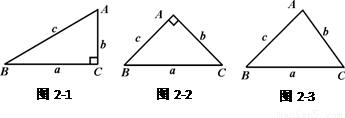
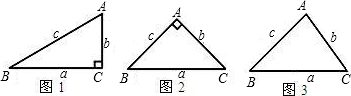
�Ķ����в��ϣ���Ҫ�������⣺��ͼ1���ڡ�ABC�У���A=2��B���ҡ�A=60�ȣ�С��ͨ�����¼��㣺�����⣬��B=30�㣬��C=90�㣬c=2b��a=
| 3 |
| 3 |
��1����ͼ2������������С���ķ������Ե���ֱ�������ν�����֤���ж�С���IJ²��Ƿ���ȷ����д����֤���̣�
��2����ͼ3������ΪС���IJ����Ƿ���ȷ������Ϊ��ȷ������֤����������˵�����ɣ�
��3����һ�������ε����߳�ǡΪ��������ż�����ҡ�A=2��B����ֱ��д��������������ߵ�
 ��������˵�����ɣ�
��������˵�����ɣ�
����������ֱ���������У���A=90�㣬c=b��a=
b������a2-b2=bc���Խ�����֤���ӳ�BA����D��ʹAD=AC=b������CD�����ACDΪ���������Σ����ݡ�ACD�ס�CBD�����������εĶ�Ӧ�ߵı���ȣ��Ϳ����������֤�Ľ��ۣ�
| 2 |
����⣺��1�������⣬�á�A=90�㣬c=b��a=
b��
��a2-b2=��
b��2-b2=b2=bc����3�֣�
��2��С���IJ�������ȷ�ģ���4�֣�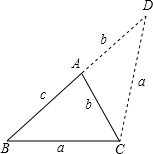
�������£���ͼ���ӳ�BA����D��ʹAD=AC=b������CD����5�֣�
���ACD����������
���BAC=2��ACD���֡�BAC=2��B��
���B=��ACD=��D��
���CBDΪ���������Σ���CD=CB=a����6�֣�
�֡�D=��D�����ACD�ס�CBD����7�֣�
��
=
��
��
=
��
��a2=b2+bc��
��a2-b2=bc����8�֣�
��3���������߳�Ϊ��������������
������������ż����2n-2��2n��2n+2��
��2n+2��2-��2n-2��2=2n��2n-2����
��ã�n=5�����������ֱ��ǣ�8��10��12��
��֪��a=12��b=8��c=10����10�֣�
| 2 |
��a2-b2=��
| 2 |
��2��С���IJ�������ȷ�ģ���4�֣�

�������£���ͼ���ӳ�BA����D��ʹAD=AC=b������CD����5�֣�
���ACD����������
���BAC=2��ACD���֡�BAC=2��B��
���B=��ACD=��D��
���CBDΪ���������Σ���CD=CB=a����6�֣�
�֡�D=��D�����ACD�ס�CBD����7�֣�
��
| AD |
| CD |
| CD |
| BD |
��
| b |
| a |
| a |
| b+c |
��a2=b2+bc��
��a2-b2=bc����8�֣�
��3���������߳�Ϊ��������������
������������ż����2n-2��2n��2n+2��
��2n+2��2-��2n-2��2=2n��2n-2����
��ã�n=5�����������ֱ��ǣ�8��10��12��
��֪��a=12��b=8��c=10����10�֣�
�������������Ĺؼ�����ȷ��ʶ����ֱ�������εıߵĹ�ϵ��֤����ACD�ס�CBD�ǽ���Ĺؼ���

��ϰ��ϵ�д�
�����Ŀ
 ���ν�ϵ�˼�뷽��
���ν�ϵ�˼�뷽��
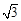 b����a2��b2��(
b����a2��b2��(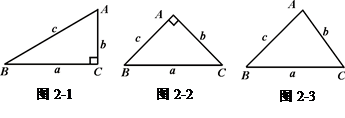
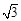 b����a2��b2��(
b����a2��b2��(