题目内容
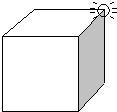如图，一只昆虫要从边长为acm的正方体盒子的一个顶点爬到相距最远的另一个顶点，沿盒子表面爬行的最短路程是分析：把此正方体的一面展开，然后在平面内，利用勾股定理求点A和B点间的线段长，即可得到蚂蚁爬行的最短距离．在直角三角形中，一条直角边长等于棱长，另一条直角边长等于两条棱长，利用勾股定理可求得．
解答：
解：如图将正方体展开，根据“两点之间，线段最短”知，线段AB即为最短路线．
展开后由勾股定理得：AB2=a2+（a+a）2=5a2，故AB=
acm，
故答案为
a．
解：如图将正方体展开，根据“两点之间，线段最短”知，线段AB即为最短路线．展开后由勾股定理得：AB2=a2+（a+a）2=5a2，故AB=
| 5 |
故答案为
| 5 |
点评：本题考查了勾股定理的拓展应用．“化曲面为平面”是解决“怎样爬行最近”这类问题的关键．
练习册系列答案
名校课堂系列答案
相关题目
，哪条路径最短？设这个正方体的边长是5 cm．
＝5
)
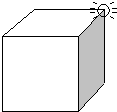如图，一只昆虫要从边长为acm的正方体盒子的一个顶点爬到相距最远的另一个顶点，沿盒子表面爬行的最短路程是________cm．