题目内容
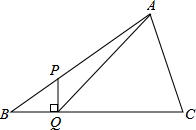（2009•郑州模拟）如图，在△ABC中，∠B=30°，点P是AB上一点，AP=2BP，PQ⊥BC于Q，连接AQ，则cos∠AQC的值为2
| ||
| 7 |
2
| ||
| 7 |
分析：过A作BC的垂线AD，根据PQ⊥BC，∠B=30°可知BP=2PQ，BQ=
PQ，故可得出△BPQ∽△BAD，再根据AP=2BP，可知AD=3PQ，DQ=2BQ=2
PQ，进而可得出
的值，设AD=
x，则DQ=2x，由勾股定理可得出AQ的值，再由cos∠AQC=
即可得出结论．
| 3 |
| 3 |
| AD |
| DQ |
| 3 |
| DQ |
| AQ |
解答：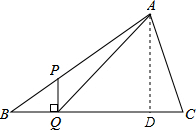
解：过A作BC的垂线AD，
∵PQ⊥BC，∠B=30°，
∴BP=2PQ，BQ=
PQ，
∵AD⊥BC，
∴△BPQ∽△BAD，
∵AP=2BP，
∴AD=3PQ，DQ=2BQ=2
PQ，
∴
=
=
，
设AD=
x，则DQ=2x，AQ=
=
=
x，
∴cos∠AQC=
=
=
．
故答案为：
．
解：过A作BC的垂线AD，∵PQ⊥BC，∠B=30°，
∴BP=2PQ，BQ=
| 3 |
∵AD⊥BC，
∴△BPQ∽△BAD，
∵AP=2BP，
∴AD=3PQ，DQ=2BQ=2
| 3 |
∴
| AD |
| DQ |
| 3PQ | ||
2
|
| ||
| 2 |
设AD=
| 3 |
| AD2+DQ2 |
(
|
| 7 |
∴cos∠AQC=
| DQ |
| AQ |
| 2x | ||
|
2
| ||
| 7 |
故答案为：
2
| ||
| 7 |
点评：本题考查的是相似三角形的判定与性质，根据题意作出辅助线，构造出相似三角形是解答此题的关键．
练习册系列答案
相关题目
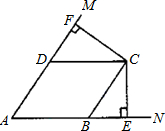（2009•郑州模拟）如图，点C是∠MAN平分线上的一点，过点C作CF⊥AM于点F，CE⊥AN于点E，过点C作CD∥AN交AM于点D，CB∥AM交AN于点B．请你判断四边形ABCD是什么特殊的四边形？请说明理由．
（2009•郑州模拟）如图，某公园管理处计划在公园里建一个以C为喷泉中心，半径为15，米的圆形喷水池．公园里已建有A、B两个休息亭，AB是一条42米长得人行道，现测得∠A=37°，∠B=45°．若要在人行道AB上安装喷泉用水控制阀E，使它到喷泉中心C的距离最短．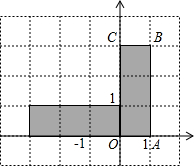
（2009•郑州模拟）如图，在平面直角坐标系中，矩形OABC各顶点都在网格格点上，现将矩形OABC绕原点逆时针90°后，点B的对应点B′的坐标为