题目内容
如图,已知1号、4号两个正方形的面积和为7,2号、3号两个正方形的面积和为4,则a,b,c三个正方形的面积和为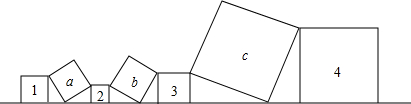
- A.11
- B.15
- C.10
- D.22
B
分析:由直角三角形的勾股定理以及正方形的面积公式,不难发现:a的面积等于1的面积加上2的面积,b的面积等于2加上3,据此可以求出三个的面积的和.
解答:利用勾股定理可得Sa=S1+S2,Sb=S2+S3,Sc=S3+S4,
∴Sa+Sb+Sc=Sa=S1+S2+S2+S3+S3+S4=7+4+4=15.
故选B.
点评:本题考查了勾股定理的运用,结合正方形的面积公式求解.
分析:由直角三角形的勾股定理以及正方形的面积公式,不难发现:a的面积等于1的面积加上2的面积,b的面积等于2加上3,据此可以求出三个的面积的和.
解答:利用勾股定理可得Sa=S1+S2,Sb=S2+S3,Sc=S3+S4,
∴Sa+Sb+Sc=Sa=S1+S2+S2+S3+S3+S4=7+4+4=15.
故选B.
点评:本题考查了勾股定理的运用,结合正方形的面积公式求解.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目

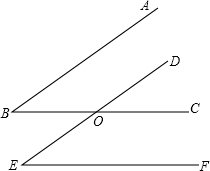 如图,已知:BC交DE于O,给出下面三个论断:①∠B=∠E;②AB∥DE;③BC∥EF.请以其中的两个论断为条件,填入“题设”栏中,以一个论断为结论,填入“结论”栏中,使之成为一个正确的命题,并加以证明.
如图,已知:BC交DE于O,给出下面三个论断:①∠B=∠E;②AB∥DE;③BC∥EF.请以其中的两个论断为条件,填入“题设”栏中,以一个论断为结论,填入“结论”栏中,使之成为一个正确的命题,并加以证明. 第二次飞行周期扩大1倍.已知三次飞行周期和为88小时,求第一、二、三次轨道飞行的周期各是多少小时?
第二次飞行周期扩大1倍.已知三次飞行周期和为88小时,求第一、二、三次轨道飞行的周期各是多少小时?