题目内容
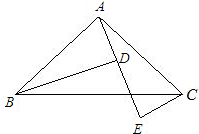 已知如图,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在DE的异侧,BD⊥AE于D,CE⊥AE于E.
已知如图,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在DE的异侧,BD⊥AE于D,CE⊥AE于E.
(1)△ABD与△CAE全等吗?请说明理由;
(2)判断BD与DE+CE关系,并请说明理由.
解:(1)△ABD与△CAE全等;
理由:∵BD⊥AE于D,CE⊥AE
∴∠ADB=∠AEC=90°,
又∵∠BAC=90°
∴∠BAD+∠EAC=90°,∠ACE+∠EAC=90°
∴∠BAD=∠ACE
在△ABD与△CAE中

∴△ABD≌△CAE.
(2)BD=DE+CE;
理由:∵△ABD≌△CAE
∴BD=AE,AD=EC
∵AE=AD+DE
∴BD=DE+CE.
分析:(1)根据等角的余角相等得出∠BAD=∠ACE,再根据AAS判定△ABD≌△CAE.
(2)根据△ABD≌△CAE,得出其对应边相等,然后得出BD=DE+CE.
点评:本题考查了全等三角形的判定及其性质,一道题目中有多个90°的角出现时,根据互余,能够得到角相等,为全等提供条件,注意运用.
理由:∵BD⊥AE于D,CE⊥AE
∴∠ADB=∠AEC=90°,
又∵∠BAC=90°
∴∠BAD+∠EAC=90°,∠ACE+∠EAC=90°
∴∠BAD=∠ACE
在△ABD与△CAE中

∴△ABD≌△CAE.
(2)BD=DE+CE;
理由:∵△ABD≌△CAE
∴BD=AE,AD=EC
∵AE=AD+DE
∴BD=DE+CE.
分析:(1)根据等角的余角相等得出∠BAD=∠ACE,再根据AAS判定△ABD≌△CAE.
(2)根据△ABD≌△CAE,得出其对应边相等,然后得出BD=DE+CE.
点评:本题考查了全等三角形的判定及其性质,一道题目中有多个90°的角出现时,根据互余,能够得到角相等,为全等提供条件,注意运用.

练习册系列答案
相关题目
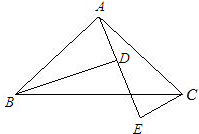 已知如图,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在DE的异侧,BD⊥AE于D,CE⊥AE于E.
已知如图,AB=AC,∠BAC=90°,AE是过A点的一条直线,且B、C在DE的异侧,BD⊥AE于D,CE⊥AE于E.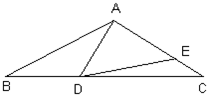
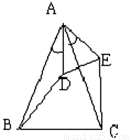
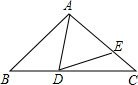 已知如图,AB=AC,AD=AE,若∠BAD=47°30′,求∠CDE的度数.
已知如图,AB=AC,AD=AE,若∠BAD=47°30′,求∠CDE的度数.