题目内容
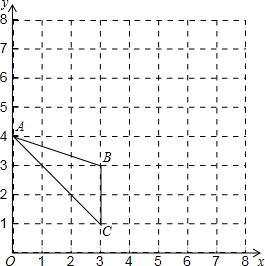 已知在正方形网格上建立的平面直角坐标系中,△ABC的位置如图所示
已知在正方形网格上建立的平面直角坐标系中,△ABC的位置如图所示(1)将△ABC绕点C顺时针方向旋转90°后得△A′B′C′
①直接写出B点的对应点B'的坐标;
②求B点旋转到点B'所经过的路线长(结果保留π)
(2)在正方形网格中,每个小正方形的顶点称为格点,在图中确定格点D,并画出以A、B、C、D为顶点的四边形,使其为中心对称图形(画一个即可).
分析:(1)①先画出旋转后的图形,然后结合直角坐标系即可得出B'的坐标;②点B所经过的路线上是弧BB'的长度;
(2)可使四边形ABCD为平行四边形.
(2)可使四边形ABCD为平行四边形.
解答:解:(1)
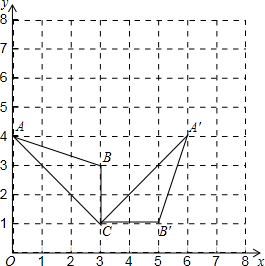
由图形可得点B'的坐标为:(5,1),
B点旋转到点B'所经过的路线长l=
=π;
(2)所画图形如下所示:
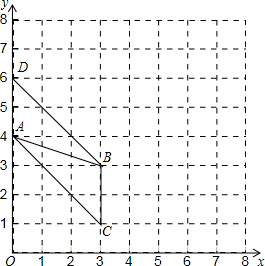 .
.

由图形可得点B'的坐标为:(5,1),
B点旋转到点B'所经过的路线长l=
| 90π×2 |
| 180 |
(2)所画图形如下所示:
 .
.点评:本题考查了旋转作图的知识,属于基础题,注意仔细审题,寻找旋转的三要素,另外要熟练掌握弧长的计算公式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的位置如图所示
的位置如图所示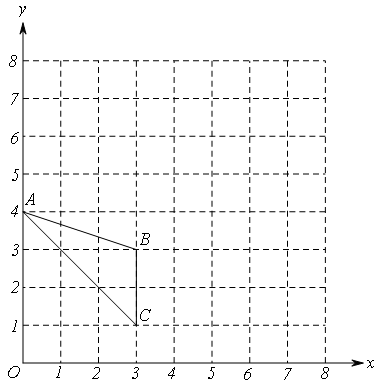
 顺时针方向旋转
顺时针方向旋转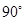 后得
后得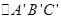
 点的对应点
点的对应点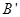 的坐标;
的坐标;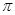 )
)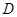 ,并画出以
,并画出以 为顶点的四边形,使其为中心对称图形(画一个即可)
为顶点的四边形,使其为中心对称图形(画一个即可) 的位置如图所示
的位置如图所示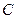 顺时针方向旋转
顺时针方向旋转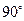 后得
后得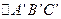
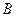 点的对应点
点的对应点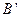 的坐标;
的坐标;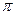 )
)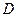 ,并画出以
,并画出以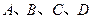 为顶点的四边形,使其为中心对称图形(画一个即可)。
为顶点的四边形,使其为中心对称图形(画一个即可)。
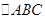 的位置如图所示
的位置如图所示 顺时针方向旋转
顺时针方向旋转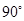 后得
后得
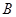 点的对应点
点的对应点 的坐标;
的坐标; )
)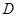 ,并画出以
,并画出以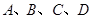 为顶点的四边形,使其为中心对称图形(画一个即可)。
为顶点的四边形,使其为中心对称图形(画一个即可)。
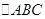 的位置如图所示
的位置如图所示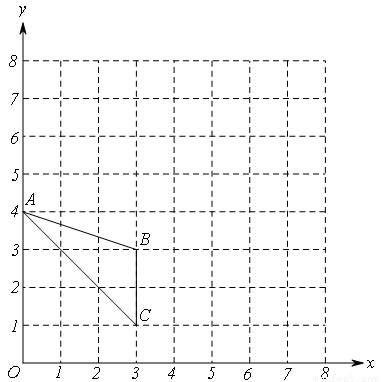
 顺时针方向旋转
顺时针方向旋转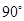 后得
后得
 点的对应点
点的对应点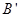 的坐标;
的坐标; )
) ,并画出以
,并画出以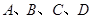 为顶点的四边形,使其为中心对称图形(画一个即可)
为顶点的四边形,使其为中心对称图形(画一个即可)