题目内容
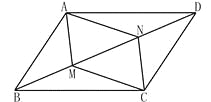
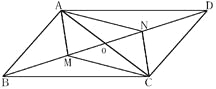
【题目】如图,M、N是平行四边形ABCD对角线BD上两点.
(1)若BM=MN=DN,求证:四边形AMCN为平行四边形;
(2)若M、N为对角线BD上的动点(均可与端点重合),设BD=12cm,点M由点B向点D匀速运动,速度为2(cm/s),同时点N由点D向点B匀速运动,速度为 a(cm/s),运动时间为t(s).若要使四边形AMCN为平行四边形,求a的值及t的取值范围.
【答案】(1)证明见解析;(2)a=2,0≤t≤6且t≠3.
【解析】
试题(1)根据题意易证△AND≌△CMB.所以AN=CM,∠AND=∠CMB.所以∠ANM=∠CMN,即AN∥CM.因此,四边形AMCN为平行四边形;
(2)连接AC,交BD于O,要使四边形AMCN为平行四边形,即OM=ON,列出方程与不等式即可求解.
试题解析:(1)∵四边形ABCD是平行四边形
∴AD=CB,AD∥BC
∴∠ADB=∠CBD
又∵BM=DN
∴△AND≌△CBM
∴CM=AN,∠BMC=∠DNA
∴∠CMN=∠ANM
∴CM∥AN
∴四边形AMCN为平行四边形;
(2)如图,连接AC,交BD于O,要使四边形AMCN为平行四边形,即OM=ON,
∴6-2t=6-at
∴a=2
当M、M重合于点O,即t=3时,点A、M、C、N在同一直线上,不能组成四边形,
∴0≤t≤6且t≠3.

练习册系列答案
相关题目