题目内容
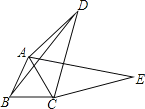
【题目】如图，△ABC为等边三角形，E为AC上一点，连接BE，将△BEC旋转，使点C落在BC上的点D处，点B落在BC上方的点F处，点E落在点C处，连接AF.求证：四边形ABDF为平行四边形.
【答案】证明见解析
【解析】
试题由旋转的性质可知FD=AB，∠EDC=∠ABC.从而可得AB//DF，根据一组对边平行且相等的四边形是平行四边形可得四边形ABDF为平行四边形
试题解析：∵△ABC是等边三角形，
∴AB="BC," ∠ABC=∠ACB=600.
∵△FCD由△BEC旋转得到的，∴CD=CE,DF=BC.
∴AB="DF"
∴△CDE是等边三角形.
∴∠EDC=600.∴∠EDC=∠ABC.
∴DF∥AB.
∴四边形ABDF是平行四边形（一组对边平行且相等的四边形是平行四边形）.
练习册系列答案
备战中考寒假系列答案
相关题目
