题目内容
商场购进某种新商品的每件进价为120元,在试销期间发现,当每件商品的售价为130元时,每天可销售70件;当每件商品的售价高于130元时,每涨价1元,日销售量就减少1件,据此规律,请回答下列问题.
(1)当每件商品的售价为140元时,每天可销售 件商品,商场每天可盈利 元;
(2)设销售价定为x元时,商品每天可销售 件,每件盈
利 元;
(3)在商品销售正常的情况下,每件商品的销售价定为多少元时,商场每天盈利可达到1500元(提示:盈利=售价-进价);
(4)能不能通过适当的降价,使商场的每天盈利达到最大.若能,请求出售价多少元时每天盈利最大,每天最大盈利为多少元(若能,可直接写出答案)?若不能,请说明理由.
(1)60, 1200
(2)(200-x), (x-120)
(3)每件商品的销售价定为150元或170元时,商场每天盈利可达到1500元.
(4)解:能.当售价160元时,每天盈利最大,每天最大盈利为1600元.
解析试题分析:(1)依题意知,当商品售价高于130元时每涨价1元日销售量减少一件。所以140-130=10(元),则涨价10元时,日销售量=70-10=60(件)。盈利=(140-120)×60=1200(元)
(2)设销售价定为x元时,商品每天可销售(200-x)件,每件盈利(x-120)元
(3)解:由题意得
(200-x)(x-120)=1500, 解得: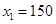 ,
,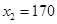 .
.
答:每件商品的销售价定为150元或170元时,商场每天盈利可达到1500元.
(4)解:能.当售价160元时,每天盈利最大,每天最大盈利为1600元. 2′
(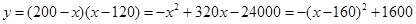 )
)
考点:二元一次方程实际应用
点评:本题难度中等,主要考查学生对运用二元一次方程解决销售问题的能力。为中考常考题型,要牢固掌握解题技巧。
