题目内容
已知PA是⊙O的切线，A为切点，PBC是过点O的割线，PA=10cm，PB=5cm，则⊙O的半径长为（ ）A．15cm
B．10cm
C．7.5cm
D．5cm
【答案】分析：根据切割线定理分析解答．
解答：解：根据切割线定理的PA2=PO•PC，
所以100=5×PC，PC=20cm，BC=20-5=15cm．
因为PBC是过点O的割线，
所以⊙O的半径长为15×
=7.5cm．
故选C．
点评：利用切割线解题时要注意BC是直径，而求得是半径，不要误选A．
解答：解：根据切割线定理的PA2=PO•PC，
所以100=5×PC，PC=20cm，BC=20-5=15cm．
因为PBC是过点O的割线，
所以⊙O的半径长为15×
=7.5cm．故选C．
点评：利用切割线解题时要注意BC是直径，而求得是半径，不要误选A．
练习册系列答案
相关题目
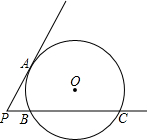如图，已知PA是⊙O的切线，A为切点，PC与⊙O相交于B、C两点，PB=2cm，BC=8cm，则PA的长等于（ ）| A、4cm | ||
| B、16cm | ||
| C、20cm | ||
D、2
|
已知PA是⊙O的切线，A为切点，PBC是割线，且AC是⊙O的直径，若PA=4，BC=6，则sin∠P的值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知PA是⊙O的切线，A为切点，PBC是过点O的割线，PA=10cm，PB=5cm，则⊙O的半径长为（ ）
| A、15cm | B、10cm | C、7.5cm | D、5cm |
9、如图，已知PA是⊙O的切线，A是切点PC是过圆心的一条割线，点B、C是它与⊙O的交点，且PA=8，PB=4．则⊙O的半径为
如图，已知PA是⊙O的切线，切点为A，PA=