题目内容
阅读并解答:
①方程x2﹣2x+1=0的根是x1=x2=1,则有x1+x2=2,x1x2=1.
②方程x2﹣x﹣2=0的根是x1=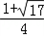 ,x2=
,x2=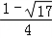 ,则有x1+x2=
,则有x1+x2= ,x1x2=﹣1.
,x1x2=﹣1.
③方程3x2+4x﹣7=0的根是x1=﹣ ,x2=1,则有x1+x2=﹣
,x2=1,则有x1+x2=﹣ ,x1x2=﹣
,x1x2=﹣ .
.
(1)根据以上①②③请你猜想:如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根为x1,x2,那么x1,x2与系数a、b、c有什么关系?请写出你的猜想并证明你的猜想;
(2)利用你的猜想结论,解决下面的问题:已知关于x的方程x2+(2k+1)x+k2﹣2=0有实数根x1,x2,且x12+x22=11,求k的值.
①方程x2﹣2x+1=0的根是x1=x2=1,则有x1+x2=2,x1x2=1.
②方程x2﹣x﹣2=0的根是x1=
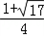 ,x2=
,x2=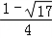 ,则有x1+x2=
,则有x1+x2= ,x1x2=﹣1.
,x1x2=﹣1.③方程3x2+4x﹣7=0的根是x1=﹣
 ,x2=1,则有x1+x2=﹣
,x2=1,则有x1+x2=﹣ ,x1x2=﹣
,x1x2=﹣ .
.(1)根据以上①②③请你猜想:如果关于x的一元二次方程ax2+bx+c=0(a≠0)有两个实数根为x1,x2,那么x1,x2与系数a、b、c有什么关系?请写出你的猜想并证明你的猜想;
(2)利用你的猜想结论,解决下面的问题:已知关于x的方程x2+(2k+1)x+k2﹣2=0有实数根x1,x2,且x12+x22=11,求k的值.
解:(1)猜想为:设ax2+bx+c=0(a≠0)的两根为x1、x2,
则有 ,
, .
.
理由:设x1、x2是一元二次方程ax2+bx+c=0(a≠0)的两根,那么由求根公式可知,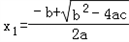 ,
,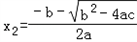 .
.
于是有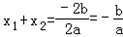 ,
,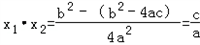 ,
,
综上得,设ax2+bx+c=0(a≠0)的两根为x1、x2,则有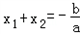 ,
,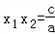 .
.
(2)x1、x2是方程x2+(2k+1)x+k2﹣2=0的两个实数根
∴x1+x2=﹣(2k+1),x1x2=k2﹣2,
又∵x12+x22=x12+x22+2x1x2﹣2x1x2=(x1+x2)2﹣2x1x2
∴[﹣(2k+1)]2﹣2×(k2﹣2)=11
整理得k2+2k﹣3=0,
解得k=1或﹣3,
又△=[﹣(2k+1)]2﹣4(k2﹣2 )≥0,解得k≥﹣ ,∴k=1.
,∴k=1.
则有
 ,
, .
.理由:设x1、x2是一元二次方程ax2+bx+c=0(a≠0)的两根,那么由求根公式可知,
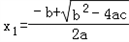 ,
,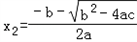 .
.于是有
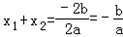 ,
,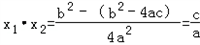 ,
,综上得,设ax2+bx+c=0(a≠0)的两根为x1、x2,则有
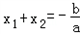 ,
,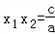 .
.(2)x1、x2是方程x2+(2k+1)x+k2﹣2=0的两个实数根
∴x1+x2=﹣(2k+1),x1x2=k2﹣2,
又∵x12+x22=x12+x22+2x1x2﹣2x1x2=(x1+x2)2﹣2x1x2
∴[﹣(2k+1)]2﹣2×(k2﹣2)=11
整理得k2+2k﹣3=0,
解得k=1或﹣3,
又△=[﹣(2k+1)]2﹣4(k2﹣2 )≥0,解得k≥﹣
 ,∴k=1.
,∴k=1.
练习册系列答案
相关题目
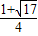 ,x2=
,x2=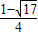 ,则有x1+x2=
,则有x1+x2= ,x1x2=-1.
,x1x2=-1. ,x2=1,则有x1+x2=-
,x2=1,则有x1+x2=- ,x1x2=-
,x1x2=- .
.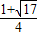 ,x2=
,x2=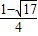 ,则有x1+x2=
,则有x1+x2= ,x1x2=-1.
,x1x2=-1. ,x2=1,则有x1+x2=-
,x2=1,则有x1+x2=- ,x1x2=-
,x1x2=- .
.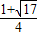 ,x2=
,x2= ,则有x1+x2=
,则有x1+x2= ,x1x2=-1.
,x1x2=-1. ,x2=1,则有x1+x2=-
,x2=1,则有x1+x2=- ,x1x2=-
,x1x2=- .
.