题目内容
一个圆桶底面直径为24cm，高32cm，则桶内所能容下的最长木棒为（ ）
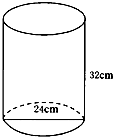
| A、20cm | B、50cm | C、40cm | D、45cm |
分析：如图，AC为圆桶底面直径，所以AC=24cm，CB=32cm，那么线段AB的长度就是桶内所能容下的最长木棒的长度，在直角三角形ABC中利用勾股定理可以求出AB，也就求出了桶内所能容下的最长木棒的长度．
解答：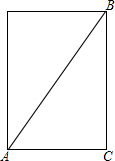
解：如图，AC为圆桶底面直径，
∴AC=24cm，CB=32cm，
∴线段AB的长度就是桶内所能容下的最长木棒的长度，
∴AB=
=40cm．
故桶内所能容下的最长木棒的长度为40cm．
故选C．
解：如图，AC为圆桶底面直径，∴AC=24cm，CB=32cm，
∴线段AB的长度就是桶内所能容下的最长木棒的长度，
∴AB=
| AC2+CB2 |
故桶内所能容下的最长木棒的长度为40cm．
故选C．
点评：此题首先要正确理解题意，把握好题目的数量关系，然后利用勾股定理即可求出结果．
练习册系列答案
相关题目
一个圆桶底面直径为10cm，高24cm，则桶内所能容下的最长木棒为（ ）
| A、20cm | B、24cm | C、26cm | D、30cm |
木棒为
C.40 cm D.45 cm