题目内容
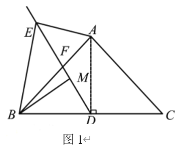
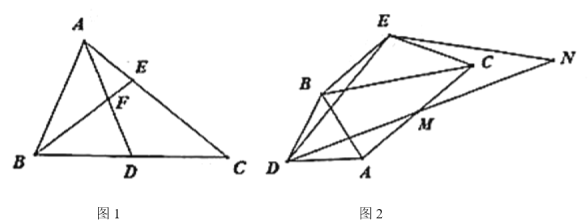
【题目】如图1,在![]() 中,
中,![]() 分别为
分别为![]() 上一点,且
上一点,且![]() ,
,![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)若![]() ,将
,将![]() 绕
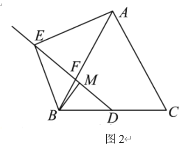
绕![]() 顺时针旋转至如图2所示位置(
顺时针旋转至如图2所示位置(![]() 不动),连
不动),连![]() ,取
,取![]() 中点
中点![]() ,连
,连![]() ,
,![]() 为射线
为射线![]() 上一点,连
上一点,连![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)由![]() 可得
可得![]() ,由
,由![]() 可得
可得![]() ,可证
,可证![]()
(2)延长![]() 至
至![]() ,使
,使![]() ,连
,连![]() ,在
,在![]() 上截取
上截取![]() ,连
,连![]() ,可证:
,可证:![]() 可得
可得![]() ,可证:
,可证:![]() 可得
可得![]() ,故
,故![]() 即可证
即可证![]()
(3)延长![]() 至
至![]() 使
使![]() ,连
,连![]() ,
,![]() ,延长
,延长![]() ,
,![]() 交于
交于![]() ,
,![]() 交
交![]() 于
于![]()
可证:![]() ,故
,故![]() ,
,![]() ,
,![]() ,由(2)知
,由(2)知![]() ,由于
,由于![]() 故可得
故可得![]() 故
故![]() ,故
,故![]() .故
.故![]() 可证
可证![]() ,可得
,可得![]() ,
,![]() 可证
可证![]() 为正三角形,故
为正三角形,故![]() ,由于
,由于![]() 故
故![]() 即可求出
即可求出![]() 的最小值.
的最小值.
(1)证明:![]()
又![]()
![]()
![]()
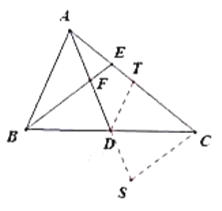
(2)证明:延长![]() 至
至![]() ,使
,使![]() ,连
,连![]() ,在
,在![]() 上截取
上截取![]() ,连
,连![]() .
.
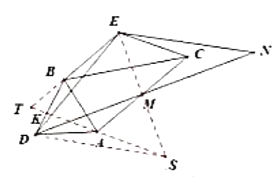
∵BD=CD,∠BDF=∠CDS
∴![]()
∵∠TCD =∠EBC
∴∠TCD=∠DCS
∵TC=SC,CD=CD
∴![]()
![]()
![]() .
.
∴![]()
(3)解:延长![]() 至
至![]() 使
使![]() ,
,
连![]() ,
,![]() ,延长
,延长![]() ,
,![]() 交于
交于![]() ,
,![]() 交
交![]() 于
于![]()
∵M是AC的中点
∴AM=MC
∵∠CME=∠SMA,EM=MS
∴![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
由(2)知![]()
![]()
![]()
![]() .
.
![]()
在![]() 和
和![]() 中
中
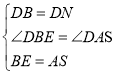
![]()
![]()
![]()
![]() 为正三角形,
为正三角形,![]()
![]()
![]() 的最小值为
的最小值为![]()

练习册系列答案
相关题目