题目内容
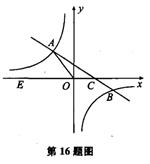
.(12分)如图,在平面直角坐标系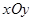 中,点
中,点 的坐标为
的坐标为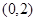 ,点
,点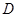 在
在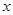 轴的正半轴上,
轴的正半轴上,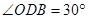 ,
,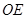 为△
为△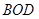 的中线,过
的中线,过 、
、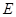 两点的抛物线
两点的抛物线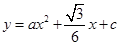 与
与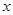 轴相交于
轴相交于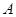 、
、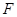 两点(
两点(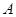 在
在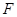 的左侧).
的左侧).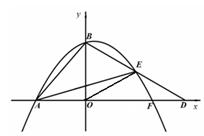
【小题1】(1)求抛物线的解析式;
【小题2】(2)等边△
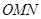 的顶点
的顶点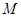 、
、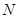 在线段
在线段 上,求
上,求 及
及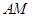 的长;
的长;【小题3】(3)点
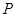 为△
为△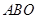 内的一个动点,设
内的一个动点,设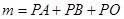 ,请直接写出
,请直接写出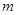 的最小值,以及
的最小值,以及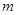 取得最小值时,线段
取得最小值时,线段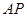 的长.
的长.
【小题1】解:(1)过
 作
作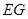 ⊥
⊥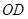 于
于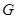 .
.∵
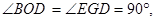
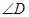 =
=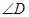 ,
,∴△
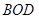 ∽△
∽△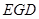 .
.∵点
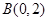 ,
,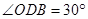 ,可得
,可得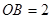 ,
,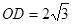 .
.∵
 为
为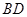 中点,
中点,∴
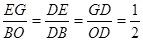 .
.∴
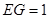 ,
,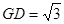 .
.∴
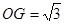 .
.∴点
 的坐标为
的坐标为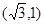 .
.∵抛物线
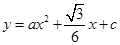 经过
经过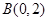 、
、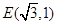 两点,
两点,∴
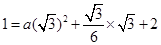 .
.可得
 .
.∴抛物线的解析式为
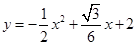 .
.【小题2】(2)∵抛物线与
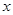 轴相交于
轴相交于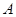 、
、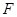 ,
,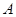 在
在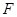 的左侧,
的左侧,∴
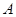 点的坐标为
点的坐标为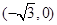 .
.∴
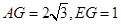 ,
,∴在△
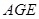 中,
中,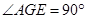 ,
,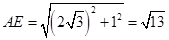 .
.过点
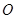 作
作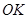 ⊥
⊥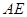 于
于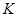 ,
,可得△
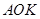 ∽△
∽△ .
.∴
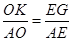 .
.∴
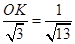 .
.∴
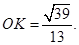
∴
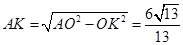 .
.∵△
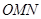 是等边三角形,
是等边三角形,∴
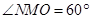 .
.∴
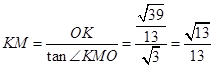 .
.∴
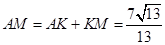 ,或
,或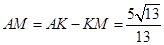
(写出一个给1分)
【小题3】(3)
 可以取到的最小值为
可以取到的最小值为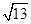 .
.当
 取得最小值时,线段
取得最小值时,线段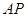 的长为
的长为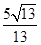 解析:
解析:略

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
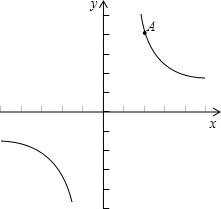
 (m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐 标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE=
(m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐 标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE=
 的图象经过点A.正比例函数y=kx的图象绕原点顺时针旋转90°后,恰好经过点A,求k的值.
的图象经过点A.正比例函数y=kx的图象绕原点顺时针旋转90°后,恰好经过点A,求k的值.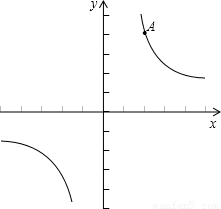
 的图象与y轴交于点A,
的图象与y轴交于点A, 的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐
的图象分别交于点M,N,已知△AOB的面积为1,点M的纵坐 时x的取值范围。
时x的取值范围。
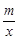 (m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐 标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE=
(m≠0)的图象交于第二、四象限内的A、B两点,与x轴交于C点,点B的坐 标为(6,n).线段OA=5,E为x轴上一点,且sin ∠AOE=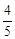 .
.