题目内容
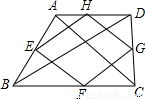
 如图,顺次连接四边形AB的各边的中点,得到四边形EFGH,在下列条件中,可使四边形EFGH为矩形的是
如图,顺次连接四边形AB的各边的中点,得到四边形EFGH,在下列条件中,可使四边形EFGH为矩形的是
- A.AB=CD
- B.AC=BD
- C.AC⊥BD
- D.AD∥BC
C
分析:根据有一个角是直角的平行四边形是矩形或有三个角是直角的四边形是矩形判断.
解答:新四边形的各边垂直,都平行于原四边形对角线,那么原四边形的对角线也应垂直.
故选C.
点评:本题考查了利用三角形中位线定理得到新四边形各边与原四边形各边的位置关系.
分析:根据有一个角是直角的平行四边形是矩形或有三个角是直角的四边形是矩形判断.
解答:新四边形的各边垂直,都平行于原四边形对角线,那么原四边形的对角线也应垂直.
故选C.
点评:本题考查了利用三角形中位线定理得到新四边形各边与原四边形各边的位置关系.

练习册系列答案
相关题目
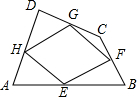 如图,顺次连接四边形ABCD各中点得四边形EFGH,要使四边形EFGH为菱形,应添加的条件是( )
如图,顺次连接四边形ABCD各中点得四边形EFGH,要使四边形EFGH为菱形,应添加的条件是( )| A、AB∥DC | B、AB=DC | C、AC⊥BD | D、AC=BD |
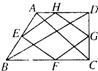 14、如图,顺次连接四边形ABCD各边中点得到四边形EFGH,要使四边形EFGH为菱形,应添加的条件是
14、如图,顺次连接四边形ABCD各边中点得到四边形EFGH,要使四边形EFGH为菱形,应添加的条件是 5、如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( )
5、如图,顺次连接四边形ABCD各边中点得四边形EFGH,要使四边形EFGH为矩形,应添加的条件是( ) 7、如图,顺次连接四边形AB的各边的中点,得到四边形EFGH,在下列条件中,可使四边形EFGH为矩形的是( )
7、如图,顺次连接四边形AB的各边的中点,得到四边形EFGH,在下列条件中,可使四边形EFGH为矩形的是( )