��Ŀ����
����Ŀ���߳�Ϊ6�ĵȱߡ�ABC�У���D��E�ֱ���AC��BC���ϣ�DE��AB��EC=2 ![]()

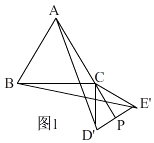
��1����ͼ1������DEC�����߷���ƽ�ƣ��õ���D��E��C�䣬��D��E����AC�Ľ���ΪM����C��D�����ACC��Ľ�ƽ���߽��ڵ�N����CC����ʱ���ı���MCND��Ϊ���Σ���˵�����ɣ�
��2����ͼ2������DEC�Ƶ�C��ת�Ϧ���0�㣼����360�㣩���õ���D��E��C������AD�䡢BE�䣮��D��E����е�ΪP��
������ת�����У�AD���BE����������������ϵ����˵�����ɣ�
������AP����AP���ʱ����AD���ֵ��������������ţ�
���𰸡�
��1��
�⣺��CC'= ![]() ʱ���ı���MCND'�����Σ�
ʱ���ı���MCND'�����Σ�
���ɣ���ƽ�Ƶ����ʵã�CD��C'D'��DE��D'E'��
�ߡ�ABC�ǵȱ������Σ�
���B=��ACB=60�㣬
���ACC'=180�㩁��ACB=120�㣬
��CN�ǡ�ACC'�Ľ�ƽ���ߣ�
���D'E'C'= ![]() ��ACC'=60��=��B��
��ACC'=60��=��B��
���D'E'C'=��NCC'��
��D'E'��CN��
���ı���MCND'��ƽ���ı��Σ�
�ߡ�ME'C'=��MCE'=60�㣬��NCC'=��NC'C=60�㣬
���MCE'�͡�NCC'�ǵȱ������Σ�
��MC=CE'��NC=CC'��
��E'C'=2 ![]() ��
��
���ı���MCND'�����Σ�
��CN=CM��
��CC'= ![]() E'C'=
E'C'= ![]()
��2��
�⣺��AD'=BE'��
���ɣ�������180��ʱ������ת�����ʵã���ACD'=��BCE'��
�ɣ�1��֪��AC=BC��CD'=CE'��
���ACD'�ա�BCE'��
��AD'=BE'��
����=180��ʱ��AD'=AC+CD'��BE'=BC+CE'��
����AD'=BE'��
���Ͽ�֪��AD'=BE'��
����ͼ����CP��
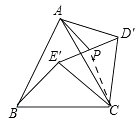
�ڡ�ACP�У������������߹�ϵ�ã�AP��AC+CP��
�൱��A��C��P���㹲��ʱ��AP���
��ͼ1���ڡ�D'CE'�У���PΪD'E���е㣬��AP��D'E'��PD'= ![]() ��
��
��CP=3��
��AP=6+3=9��
��Rt��APD'�У��ɹ��ɶ����ã�AD'= ![]() =2
=2 ![]() ��
��
����������1�����жϳ��ı���MCND'Ϊƽ���ı��Σ��������ε����ʵó�CN=CM���������CC'����2���ٷ����������������ת�����ʣ������жϳ���ACD�ա�BCE'���ɵó����ۣ�
�����жϳ���A��C��P���㹲�ߣ������CP��AP������ù��ɶ������ɵó����ۣ�
�����㾫�����������⣬������Ҫ�˽�ȱ������ε�����(�ȱ������ε������Ƕ���Ȳ���ÿ���Ƕ���60��)��







