题目内容
【题目】如图,直线![]() 的解析式为y=
的解析式为y=![]() x+4,与x轴y轴分别交于A,B两点;直线
x+4,与x轴y轴分别交于A,B两点;直线![]() 与x轴交于点C(2,0)与y轴交于点D(0,
与x轴交于点C(2,0)与y轴交于点D(0, ![]() ),两直线交于点P.
),两直线交于点P.
(1)求点A,B的坐标及直线![]() 的解析式;
的解析式;
(2)求证:△AOB≌△APC;
(3)若将直线![]() 向右平移m个单位,与x轴,y轴分别交于点
向右平移m个单位,与x轴,y轴分别交于点![]() 、
、![]() ,使得以点A、B、
,使得以点A、B、![]() 、
、![]() 为顶点的图形是轴对称图形,求m的值?
为顶点的图形是轴对称图形,求m的值?

【答案】(1)A(-3,0),B(0,4),l2: ![]() ;(2)证明见解析;(3)m=1.
;(2)证明见解析;(3)m=1.
【解析】试题分析:(1)根据直线![]() 的解析式为y=
的解析式为y=![]() x+4,分别令x=0、y=0即可得出A、B坐标,直线
x+4,分别令x=0、y=0即可得出A、B坐标,直线![]() 利用待定系数法即可求得;
利用待定系数法即可求得;
(2)连接AD,先证明△ADB≌△ADC,得到∠ABO=∠ACP,再根据ASA证明△AOB≌△APC即可;
(3)由B、D′都在y轴上,A、C′在x轴上,可知要想使得以点A、B、C′、D′为顶点的图形是轴对称图形,必有A、C′关于y轴对称,从而得解.
试题解析:(1)当x=0时,y=![]() x+4=4,当y=0时,0=
x+4=4,当y=0时,0=![]() x+4,解得:x=-3,
x+4,解得:x=-3,
∴A(-3,0),B(0,4),
设直线![]() 的解析式为:y=kx+b,由题意得:
的解析式为:y=kx+b,由题意得: 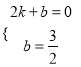 ,解得:
,解得: 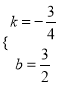 ,
,
∴直线![]() :y=
:y=![]() ;
;
(2)连接AD,
由B(0,4),D(0, ![]() ),A(-3,0),C(2,0)可得:BD=
),A(-3,0),C(2,0)可得:BD=![]() ,AC=AB=5,
,AC=AB=5,
又由OC=2,OD=![]() 得CD=
得CD=![]() =
=![]() =BD,
=BD,
在△ADB和△ADC中 ,∴△ADB≌△ADC,∴∠ABO=∠ACP,
,∴△ADB≌△ADC,∴∠ABO=∠ACP,
在△AOB和△APC中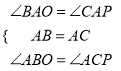 ,∴△AOB≌△APC;
,∴△AOB≌△APC;
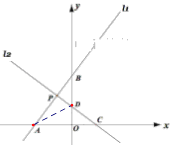
(3)∵B、D′都在y轴上,A、C′在x轴上,
∴要想使得以点A、B、C′、D′为顶点的图形是轴对称图形,必有A、C′关于y轴对称,
∴C′(3,0),
∵C(2,0),
∴m=3-2=1.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目



