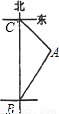题目内容
 小明骑自行车以15千米/小时的速度在公路上向正北方向匀速行进,如图,出发时,在B点他观察到仓库A在他的北偏东30°处,骑行20分钟后到达C点,发现此时这座仓库正好在他的东南方向,则这座仓库到公路的距离为
小明骑自行车以15千米/小时的速度在公路上向正北方向匀速行进,如图,出发时,在B点他观察到仓库A在他的北偏东30°处,骑行20分钟后到达C点,发现此时这座仓库正好在他的东南方向,则这座仓库到公路的距离为| 3 |
分析:过点A作AD⊥BC于点D,运用三角函数定义求AD的长.
解答: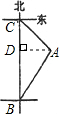 解:过点A作AD⊥BC于点D.
解:过点A作AD⊥BC于点D.
设AD=x,则BD=
x.
∵△ACD是等腰直角三角形,
∴CD=AD=x.
∵小明骑自行车以15千米/小时的速度在公路上向正北方向匀速行进,骑行20分钟后到达C点,
∴15×
=5,
∴BC=5.
∴
x+x=5.
∴x=
≈1.8(千米).
即仓库到公路的距离为1.8千米.
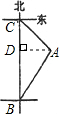 解:过点A作AD⊥BC于点D.
解:过点A作AD⊥BC于点D.设AD=x,则BD=
| 3 |
∵△ACD是等腰直角三角形,
∴CD=AD=x.
∵小明骑自行车以15千米/小时的速度在公路上向正北方向匀速行进,骑行20分钟后到达C点,
∴15×
| 20 |
| 60 |
∴BC=5.
∴
| 3 |
∴x=
5(
| ||
| 2 |
即仓库到公路的距离为1.8千米.
点评:解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
相关题目
 (2007•攀枝花)如图,小明骑自行车以15千米/小时的速度在公路上一直向正北方向匀速行进,出发时,他在B点观察到仓库A在他的北偏东25°的方向上,骑行40分钟后到达C点,他此时发现这座仓库正好在他的南偏东65°的方向上,请你求出仓库到公路的距离.(结果保留两个有效数字.可能用到的数据:sin25°=0.4226,cos25°=0.9063,sin65°=0.9063,sin75°=0.9659)
(2007•攀枝花)如图,小明骑自行车以15千米/小时的速度在公路上一直向正北方向匀速行进,出发时,他在B点观察到仓库A在他的北偏东25°的方向上,骑行40分钟后到达C点,他此时发现这座仓库正好在他的南偏东65°的方向上,请你求出仓库到公路的距离.(结果保留两个有效数字.可能用到的数据:sin25°=0.4226,cos25°=0.9063,sin65°=0.9063,sin75°=0.9659)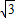 ≈1.732,结果保留两位有效数字)
≈1.732,结果保留两位有效数字)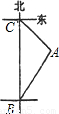
 ≈1.732,结果保留两位有效数字)
≈1.732,结果保留两位有效数字)
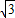 ≈1.732,结果保留两位有效数字)
≈1.732,结果保留两位有效数字)