题目内容
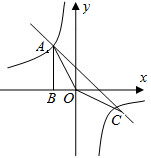 如图,Rt△ABO的顶点A是双曲线y=
如图,Rt△ABO的顶点A是双曲线y=| k |
| x |
| 3 |
| 2 |
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A、C的坐标;
(3)求△AOC的面积;
(4)根据图象写出使一次函数的值大于反比例函数的值x的取值范围.
分析:(1)先根据反比例函数的图象所在的象限判断出k的符号,在由△ABO的面积求出k的值,进而可得出两个函数的解析式;
(2)把两函数的解析式组成方程组,求出xy的值,即可得出A、C两点的坐标;
(3)由一次函数的解析式求出直线与x轴的交点,由S△AOC=S△AOD+S△COD进行解答即可.
(4)直接根据一次函数与反比例函数的交点坐标求出一次函数的值大于反比例函数的值x的取值范围即可.
(2)把两函数的解析式组成方程组,求出xy的值,即可得出A、C两点的坐标;
(3)由一次函数的解析式求出直线与x轴的交点,由S△AOC=S△AOD+S△COD进行解答即可.
(4)直接根据一次函数与反比例函数的交点坐标求出一次函数的值大于反比例函数的值x的取值范围即可.
解答: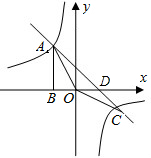 解:(1)∵反比例函数y=
解:(1)∵反比例函数y=
的图象在二、四象限,
∴k<0,
∵S△ABO=
|k|=
,
∴k=-3,
∴双曲线y=
的解析式为:y=-
;
直线y=-x-(k+1)的解析式为:y=-x-(-3+1),即y=-x+2;
(2)∵把一次函数与反比例函数的解析式组成方程组得:
,
解得
或
,
∴A(-1,3),C(3,-1);
(3)∵一次函数的解析式为:y=-x+2,
∴令y=0,则-x+2=0,即x=2,
∴直线AC与x轴的交点D(2,0),
∵A(-1,3),C(3,-1),
∴S△AOC=S△AOD+S△COD=
×2×(3+1)=4;
(4)∵A(-1,3),C(3,-1),
∴当x<-1或0<x<3时,一次函数的值大于反比例函数的值.
 解:(1)∵反比例函数y=
解:(1)∵反比例函数y=| k |
| x |
∴k<0,
∵S△ABO=
| 1 |
| 2 |
| 3 |
| 2 |
∴k=-3,
∴双曲线y=
| k |
| x |
| 3 |
| x |
直线y=-x-(k+1)的解析式为:y=-x-(-3+1),即y=-x+2;
(2)∵把一次函数与反比例函数的解析式组成方程组得:
|
解得
|
|
∴A(-1,3),C(3,-1);
(3)∵一次函数的解析式为:y=-x+2,
∴令y=0,则-x+2=0,即x=2,
∴直线AC与x轴的交点D(2,0),
∵A(-1,3),C(3,-1),
∴S△AOC=S△AOD+S△COD=
| 1 |
| 2 |
(4)∵A(-1,3),C(3,-1),
∴当x<-1或0<x<3时,一次函数的值大于反比例函数的值.
点评:本题考查的是反比例函数与一次函数的交点问题,待定系数法求一次函数及反比例函数的解析式,能根据△ABO的面积求出k的值是解答此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
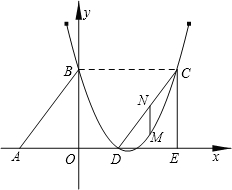 如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=
如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y= 象在第四象限的交点,AB⊥x轴于B,且S△ABO=
象在第四象限的交点,AB⊥x轴于B,且S△ABO= 标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y=
标原点,A、B两点的坐标分别为(-3,0)、(0,4),抛物线y= 如图,Rt△ABO的顶点A是反比例函数y=
如图,Rt△ABO的顶点A是反比例函数y=