题目内容
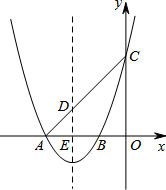 如图,已知抛物线y=x2+4x+3交x轴于A,B两点,交y轴于点C,抛物线的对称轴交x轴于点E,连接CA,交抛物线的对称轴于点D.
如图,已知抛物线y=x2+4x+3交x轴于A,B两点,交y轴于点C,抛物线的对称轴交x轴于点E,连接CA,交抛物线的对称轴于点D.(1)求抛物线的对称轴及点A的坐标.
(2)点M是线段AC下方抛物线上一点,作MN∥y轴,交AC于点N,是否存在点M,使得CN=OM?若存在,请求出点M的坐标;若不存在,请说明理由.
(3)过点B作BF∥y轴,交AC于点F.点P是抛物线上一动点,点Q是直线DE上一动点.是否存在点P,使得A,F,P,Q四点构成一个平行四边形?若存在,请求出P点的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:压轴题,存在型,分类讨论
分析:(1)根据二次函数对称轴公式列式计算即可得解,令y=0,解关于x的一元二次方程,即可得到点A的坐标;
(2)令x=0求出点C的坐标,从而得到直线AC的解析式,判断出AC与y轴的夹角度数,再根据CN=OM判断出四边形MNCO是等腰梯形或平行四边形,然后写出直线OM的解析式,再与二次函数解析式联立求解即可得到点M的坐标;
(3)写出点B的坐标,然后根据平行四边形的对边平行且相等,分①点P在对称轴左边时求出点P的横坐标,然后代入二次函数解析式计算即可求出点P的坐标,②点P在对称轴右边时,求出点P的横坐标,判断出点P与点C重合,③AF是对角线时,点P为二次函数的顶点坐标.
(2)令x=0求出点C的坐标,从而得到直线AC的解析式,判断出AC与y轴的夹角度数,再根据CN=OM判断出四边形MNCO是等腰梯形或平行四边形,然后写出直线OM的解析式,再与二次函数解析式联立求解即可得到点M的坐标;
(3)写出点B的坐标,然后根据平行四边形的对边平行且相等,分①点P在对称轴左边时求出点P的横坐标,然后代入二次函数解析式计算即可求出点P的坐标,②点P在对称轴右边时,求出点P的横坐标,判断出点P与点C重合,③AF是对角线时,点P为二次函数的顶点坐标.
解答:解:(1)对称轴:直线x=-
=-2,
令y=0,则x2+4x+3=0,
解得x1=-1,x2=-3,
所以,A(-3,0);
(2)存在.
令x=0,则y=3,
所以,点C(0,3),
∴直线AC的解析式为y=x+3,
∴直线AC与y轴的夹角为45°,
∵CN=OM,
∴四边形MNCO是等腰梯形或平行四边形,
当四边形MNCO是等腰梯形时,直线OM的解析式为y=-x,
联立
,
消掉y得,x2+5x+3=0,
解得x1=
,x2=
(舍去),
y=-x=
,
此时,点M(
,
),
当四边形MNCO是平行四边形时,直线OM的解析式为y=x,
联立
,
消掉y得,x2+3x+3=0,
△=32-4×1×3=-3<0,
方程无解,
综上所述,点M(
,
);
(3)存在.
由(1)可得点B(-1,0),
①点P在对称轴左边时,点P的横坐标为-3-1=-4,
点P的纵坐标为y=(-4)2+4×(-4)+3=3
∴P1(-4,3),
②点P在对称轴右边时,点P的横坐标为-1+1=0,
此时,点P与点C重合,A、F、P、Q四点共线,不能构成平行四边形,
③AF是对角线时,∵A(-3,0),B(-1,0),
∴点D是AF的中点,
∴点P在直线QD上,
即点P在对称轴上,
∴点P为二次函数的顶点坐标,
∵y=x2+4x+3=(x+2)2-1,
∴二次函数顶点坐标为(-2,-1),
∴点P2(-2,-1),
综上所述,P1(-4,3),P2(-2,-1).
| 4 |
| 2×1 |
令y=0,则x2+4x+3=0,
解得x1=-1,x2=-3,
所以,A(-3,0);
(2)存在.
令x=0,则y=3,
所以,点C(0,3),
∴直线AC的解析式为y=x+3,

∴直线AC与y轴的夹角为45°,
∵CN=OM,
∴四边形MNCO是等腰梯形或平行四边形,
当四边形MNCO是等腰梯形时,直线OM的解析式为y=-x,
联立
|
消掉y得,x2+5x+3=0,
解得x1=
-5+
| ||
| 2 |
-5-
| ||
| 2 |
y=-x=
5-
| ||
| 2 |
此时,点M(
-5+
| ||
| 2 |
5-
| ||
| 2 |
当四边形MNCO是平行四边形时,直线OM的解析式为y=x,
联立
|
消掉y得,x2+3x+3=0,
△=32-4×1×3=-3<0,
方程无解,
综上所述,点M(
-5+
| ||
| 2 |
5-
| ||
| 2 |
(3)存在.
由(1)可得点B(-1,0),

①点P在对称轴左边时,点P的横坐标为-3-1=-4,
点P的纵坐标为y=(-4)2+4×(-4)+3=3
∴P1(-4,3),
②点P在对称轴右边时,点P的横坐标为-1+1=0,
此时,点P与点C重合,A、F、P、Q四点共线,不能构成平行四边形,
③AF是对角线时,∵A(-3,0),B(-1,0),
∴点D是AF的中点,
∴点P在直线QD上,
即点P在对称轴上,
∴点P为二次函数的顶点坐标,
∵y=x2+4x+3=(x+2)2-1,
∴二次函数顶点坐标为(-2,-1),
∴点P2(-2,-1),
综上所述,P1(-4,3),P2(-2,-1).
点评:本题是二次函数综合题型,主要利用了二次函数的对称轴公式,二次函数与坐标轴的交点的求法,等腰梯形的两腰相等,平行四边形的对边平行且相等的性质,难点在于(3)要分情况讨论.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
观察下列图形:

它们是按一定规律排列,依照此规律,第20个图形共有?( )

它们是按一定规律排列,依照此规律,第20个图形共有?( )
| A、58个 | B、60个 |
| C、62个 | D、64个 |
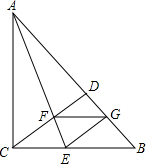 在Rt△ABC中,CD是斜边AB上的高,∠BAC的平分线AE交CD于F,交BC于E,EG⊥AB于G,求证:四边形CFGE是菱形.
在Rt△ABC中,CD是斜边AB上的高,∠BAC的平分线AE交CD于F,交BC于E,EG⊥AB于G,求证:四边形CFGE是菱形. 在下面的横线上填上推理的根据,
在下面的横线上填上推理的根据, 如图,平行四边形ABCD的对角线AC,BD相交于点O,且AC+BD=36,AB=11,求△OCD的周长.
如图,平行四边形ABCD的对角线AC,BD相交于点O,且AC+BD=36,AB=11,求△OCD的周长.