题目内容
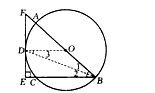
如图所示,AB是圆O的直径,CB是圆O的弦,D是 的中点,过点D作直线与BC垂直,交BC延长线于E点,且交BA延长线于F点。
的中点,过点D作直线与BC垂直,交BC延长线于E点,且交BA延长线于F点。
(1)求证:EF是圆O的切线;
(2)若tan B= ,BE=6,求圆O的半径。
,BE=6,求圆O的半径。
 的中点,过点D作直线与BC垂直,交BC延长线于E点,且交BA延长线于F点。
的中点,过点D作直线与BC垂直,交BC延长线于E点,且交BA延长线于F点。(1)求证:EF是圆O的切线;
(2)若tan B=
 ,BE=6,求圆O的半径。
,BE=6,求圆O的半径。 
| 解:(1)如图,连结OD,BD, ∵DE⊥BC, ∴∠E=90° ∵D是  的中点, 的中点,∴∠1=∠2, ∵OB=OD, ∴∠1=∠3, ∴∠2=∠3, ∴OD∥ BE, ∴∠FDO=∠E=90°, ∴EF是⊙O的切线; |
 |
(2)在Rt△BEF中,∠E=90°,tan∠ABC=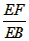 = =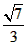 ,BE=6, ,BE=6,∴ 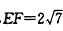 由勾股定理,有FB= 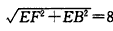 由(1)知OD∥BE, ∴△FOD∽△FBE, ∴ 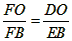 , ,设OD=x,FO=8-x ∴ 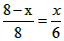 , , 解得x= 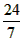 , , 即⊙的半径为 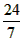 。 。 |

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
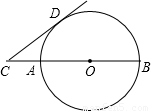
 13、如图所示,AB是圆O的直径,C是BA延长线上一点,CD切圆O于点D,CD=4,CA=2,则圆O的半径为
13、如图所示,AB是圆O的直径,C是BA延长线上一点,CD切圆O于点D,CD=4,CA=2,则圆O的半径为