题目内容
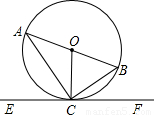
(2005•漳州)已知:如图,直线EF与⊙O相切于点C,AB是⊙O的直径,且BC=3,Ac=4.(1)求半径OC的长;
(2)在切线EF上找一点M,使得以B、M、C为顶点的三角形与△ACO相似.
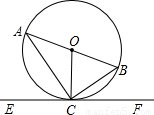
【答案】分析:(1)由于OC是半径,因此可在Rt△ACB中,利用勾股定理求得直径AB长即可;
(2)由弦切角定理知:∠BCF=∠A,因此只需令∠CBM=∠OCA即可,由于△AOC是等腰三角形,若存在M点,则△BMC也必为等腰三角形,因此M点可能有两种情况:①M点为BC垂直平分线与EF的交点;②以B为圆心,BC为半径作弧,与EF的交点即为M点.
解答:解:(1)∵AB是⊙O的直径
∴∠ACB=90°
∵BC=3,AC=4
∴AB=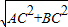 =5
=5
∴OC= AB=
AB= ;
;
(2)∵EF是⊙O的切线,
∴∠BCF=∠A,
因此点M必在射线CF上,
设点M在射线CF上,截取CM1=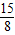 ,CM2=
,CM2=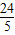 ,
,
那么点M1、M2为符合条件的点M.
点评:本题考查的是圆周角定理、切线的性质、相似三角形的判定和性质;需注意的是题中的相似三角形没有告诉对应顶点,应分情况进行讨论.
(2)由弦切角定理知:∠BCF=∠A,因此只需令∠CBM=∠OCA即可,由于△AOC是等腰三角形,若存在M点,则△BMC也必为等腰三角形,因此M点可能有两种情况:①M点为BC垂直平分线与EF的交点;②以B为圆心,BC为半径作弧,与EF的交点即为M点.
解答:解:(1)∵AB是⊙O的直径
∴∠ACB=90°
∵BC=3,AC=4
∴AB=
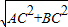 =5
=5∴OC=
 AB=
AB= ;
;(2)∵EF是⊙O的切线,
∴∠BCF=∠A,
因此点M必在射线CF上,
设点M在射线CF上,截取CM1=
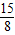 ,CM2=
,CM2=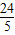 ,
,那么点M1、M2为符合条件的点M.
点评:本题考查的是圆周角定理、切线的性质、相似三角形的判定和性质;需注意的是题中的相似三角形没有告诉对应顶点,应分情况进行讨论.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 (2005•漳州)已知:如图,在坐标平面内,A(0,0),B(12,0),C(12,6),D(0,6),点Q沿DA边从点D开始向点A以1单位/秒的速度移动.点P沿AB边从点A开始向B以2单位/秒的速度移动,假设P、Q同时出发,t表示移动的时间(0≤t≤6).
(2005•漳州)已知:如图,在坐标平面内,A(0,0),B(12,0),C(12,6),D(0,6),点Q沿DA边从点D开始向点A以1单位/秒的速度移动.点P沿AB边从点A开始向B以2单位/秒的速度移动,假设P、Q同时出发,t表示移动的时间(0≤t≤6).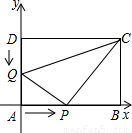 (2005•漳州)已知:如图,在坐标平面内,A(0,0),B(12,0),C(12,6),D(0,6),点Q沿DA边从点D开始向点A以1单位/秒的速度移动.点P沿AB边从点A开始向B以2单位/秒的速度移动,假设P、Q同时出发,t表示移动的时间(0≤t≤6).
(2005•漳州)已知:如图,在坐标平面内,A(0,0),B(12,0),C(12,6),D(0,6),点Q沿DA边从点D开始向点A以1单位/秒的速度移动.点P沿AB边从点A开始向B以2单位/秒的速度移动,假设P、Q同时出发,t表示移动的时间(0≤t≤6).