题目内容
 在Rt△BAC中,∠BAC=90°,cos∠ACB=
在Rt△BAC中,∠BAC=90°,cos∠ACB=| 1 |
| 4 |
考点:旋转的性质
专题:
分析:根据旋转的性质可得AC=CE,BC=CF,∠ACE=∠BCF,再根据等腰三角形两底角相等求出∠CAD=∠CBF,从而得到△ACD和△BGD相似,根据相似三角形对应边成比例求出BD=BG,过点A作AH⊥CD于H,根据等腰三角形三线合一的性质可得CD=2CH,再解直角三角形求出CH,BC,然后根据BD=BC-CD代入数据进行计算即可得解.
解答: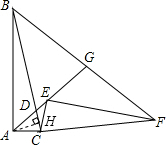 解:∵△ABC以点C为旋转中心顺时针旋转得到△EFC,
解:∵△ABC以点C为旋转中心顺时针旋转得到△EFC,
∴AC=CE,BC=CF,∠ACE=∠BCF(为旋转角),
∵∠CAD=
(180°-∠ACE),∠CBF=
(180°-∠BCF),
∴∠CAD=∠CBF,
又∵∠ADC=∠BDG,
∴△ACD∽△BGD,
∴
=
,
∵AC=AD,
∴BG=BD,
过点A作AH⊥CD于H,则CD=2CH,
∵cos∠ACB=
,AC=4,
∴
=
=
,
即
=
=
,
解得CH=1,BC=16,
∴CD=2×1=2,
BD=BC-CD=16-2=14,
∴BG=14.
故答案为:14.
 解:∵△ABC以点C为旋转中心顺时针旋转得到△EFC,
解:∵△ABC以点C为旋转中心顺时针旋转得到△EFC,∴AC=CE,BC=CF,∠ACE=∠BCF(为旋转角),
∵∠CAD=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠CAD=∠CBF,
又∵∠ADC=∠BDG,
∴△ACD∽△BGD,
∴
| AC |
| AD |
| BG |
| BD |
∵AC=AD,
∴BG=BD,
过点A作AH⊥CD于H,则CD=2CH,
∵cos∠ACB=
| 1 |
| 4 |
∴
| CH |
| AC |
| AC |
| BC |
| 1 |
| 4 |
即
| CH |
| 4 |
| 4 |
| BC |
| 1 |
| 4 |
解得CH=1,BC=16,
∴CD=2×1=2,
BD=BC-CD=16-2=14,
∴BG=14.
故答案为:14.
点评:本题考查了旋转的性质,等腰三角形两底角相等的性质,等腰三角形三线合一的性质,解直角三角形,求出BG=BD是解题的关键,也是本题的难点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
一个正数的平方根是2a-1和a-2,则这个数是( )
| A、1 | B、4 | C、9 | D、16 |
 如图,在平面直角坐标系xOy中,反比例函数
如图,在平面直角坐标系xOy中,反比例函数