题目内容
要测量河两岸相对两棵树A,B之间的距离,王立同学从A点沿垂直AB的方向前进到C点,测得∠ACB=45°.继续沿AC方向前进30 m到点D,此时沿得∠ADB=30°.依据这些数据能否求出两树之间的距离AB?若能,写出求解过程;不能,说明理由.(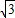 取1.73,精确到0.1 m)
取1.73,精确到0.1 m)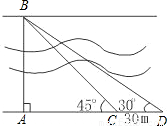
【答案】分析:图中有两个直角三角形,根据条件可表示出直角边的关系,因为CD=AD-AC=30,据此得出方程求解.
解答:解:设AB为x m
∴AC=AB=x m
∵CD=30 m
∴AD=(x+30)m
在Rt△ABC中,tan30°=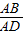
∴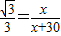 ,∴x≈41.0(m)
,∴x≈41.0(m)
答:两树间的距离约为41.0 m.
点评:当有几个直角三角形共一边时,通常通过这条公共边把不同三角形中的边联系起来,建立关系式求解.
解答:解:设AB为x m
∴AC=AB=x m
∵CD=30 m
∴AD=(x+30)m
在Rt△ABC中,tan30°=
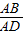
∴
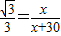 ,∴x≈41.0(m)
,∴x≈41.0(m)答:两树间的距离约为41.0 m.
点评:当有几个直角三角形共一边时,通常通过这条公共边把不同三角形中的边联系起来,建立关系式求解.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
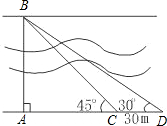 要测量河两岸相对两棵树A,B之间的距离,王立同学从A点沿垂直AB的方向前进到C点,测得∠ACB=45°.继续沿AC方向前进30 m到点D,此时沿得∠ADB=30°.依据这些数据能否求出两树之间的距离AB?若能,写出求解过程;不能,说明理由.(
要测量河两岸相对两棵树A,B之间的距离,王立同学从A点沿垂直AB的方向前进到C点,测得∠ACB=45°.继续沿AC方向前进30 m到点D,此时沿得∠ADB=30°.依据这些数据能否求出两树之间的距离AB?若能,写出求解过程;不能,说明理由.(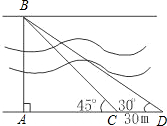 要测量河两岸相对两棵树A,B之间的距离,王立同学从A点沿垂直AB的方向前进到C点,测得∠ACB=45°.继续沿AC方向前进30 m到点D,此时沿得∠ADB=30°.依据这些数据能否求出两树之间的距离AB?若能,写出求解过程;不能,说明理由.(
要测量河两岸相对两棵树A,B之间的距离,王立同学从A点沿垂直AB的方向前进到C点,测得∠ACB=45°.继续沿AC方向前进30 m到点D,此时沿得∠ADB=30°.依据这些数据能否求出两树之间的距离AB?若能,写出求解过程;不能,说明理由.( 取1.73,精确到0.1 m)
取1.73,精确到0.1 m)