题目内容
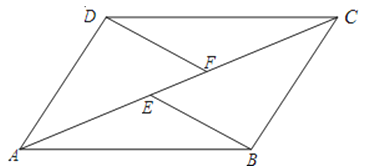
【题目】如图,在矩形ABCD中,AB=a,AD=b,E,F分别是AB,CD的中点,M是BC上一动点,AM,DM分别交EF于点G,H,连接CH.
(1)试判断GH是否为定值,并证明你的结论;
(2)当点M为BC的中点时,求证:四边形GMCH是平行四边形;
(3)试探究:在(2)的条件下,当a,b满足什么数量关系时,四边形GMCH是菱形?(不必证明,直接写出结论)
【答案】(1)解:GH=![]() b,是定值,
b,是定值,
理由:∵E,F分别是AB,CD的中点,
∴AE∥DF且AE=DF,
∴四边形AEFD是平行四边形,
∴AD∥EF∥BC,
∴![]() =
=![]() =
=![]() ,
,
∴AG=MG,DH=MH,
∴GH=![]() AD=
AD=![]() b,是定值;
b,是定值;
(2)证明:∵点M为BC的中点,
∴MC=![]() BC=
BC=![]() b,
b,
∵GH=![]() b,
b,
∴GH=CM,
又∵GH∥CM,
∴四边形GMCH是平行四边形;
(3)解:a=![]() b时,四边形GMCH是菱形.
b时,四边形GMCH是菱形.
【解析】所有
(1)利用平行四边形的判定方法得出四边形AEFD是平行四边形,进而利用平行四边形的性质得出答案;
(2)利用平行四边形的判定方法一组对边平行且相等的四边形是平行四边形得出即可;
(3)利用当a=![]() b时,由题意得出MC=BM=
b时,由题意得出MC=BM=![]() b,AM=b,则MG=
b,AM=b,则MG=![]() b,进而利用(2)中所求得出答案.
b,进而利用(2)中所求得出答案.
【考点精析】关于本题考查的菱形的判定方法,需要了解任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形才能得出正确答案.

 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案【题目】“滴滴快车”是一种便捷的出行工具,计价规则如下表:
计费项目 | 里程费 | 时长费 |
单价 | 1.4元/千米 | 0.5元/分钟 |
注:车费由里程费、时长费两部分构成,其中里程费按行车的实际里程计费,时长费按行车的实际时间计算。车费不足8元的按最低消费8元收取。为了推广和扩大“滴滴快车”的市场占有率,公司近期推出优惠政策,凡车费满10元,将给予8折优惠。 | ||
随着互联网的不断发展,更多的人们选择了“滴滴快车”出行。假设“滴滴快车”的平均行车速度为50 km/h,请回答下列问题:
(1)小明和小冰各自乘坐“滴滴快车”,行车里程分别为3千米和10千米,请问他们各自需付车费多少钱?
(2)张老师与王老师的家和学校在同一条直线上,位置如图所示.一天,张老师和王老师各自从学校“滴滴快车”回家,分别付车费9.6元和24元.请问,张老师和王老师的家相距多少千米?
![]()