题目内容
(2006•常德)如图,在直角坐标系中,已知点A( ,0),B(-
,0),B(- ,0),以点A为圆心,AB为半径的圆与x轴相交于点B,C,与y轴相交于点D,E.
,0),以点A为圆心,AB为半径的圆与x轴相交于点B,C,与y轴相交于点D,E.(1)若抛物线y=
 x2+bx+c经过C,D两点,求抛物线的解析式,并判断点B是否在该抛物线上;
x2+bx+c经过C,D两点,求抛物线的解析式,并判断点B是否在该抛物线上;(2)在(1)中的抛物线的对称轴上求一点P,使得△PBD的周长最小;
(3)设Q为(1)中的抛物线的对称轴上的一点,在抛物线上是否存在这样的点M,使得四边形BCQM是平行四边形?若存在,求出点M的坐标;若不存在,说明理由.

【答案】分析:(1)根据A( ,0),B(-
,0),B(- ,0)可求圆半径是2
,0)可求圆半径是2 ,连接AD,在Rt△AOD中,可求OD,即D(0,-3),把C,D两点坐标代入抛物线y=
,连接AD,在Rt△AOD中,可求OD,即D(0,-3),把C,D两点坐标代入抛物线y= x2+bx+c,可求抛物线解析式,将B点坐标代入解析式进行检验即可;
x2+bx+c,可求抛物线解析式,将B点坐标代入解析式进行检验即可;
(2)由(1)知,点B关于抛物线对称轴的对称点为点C,连接CD,交抛物线对称轴于P点,P点即为所求,先求直线CD的解析式,已知P点横坐标x= ,代入直线CD的解析式即可求P;
,代入直线CD的解析式即可求P;
(3)∵BC=4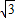 ,Q点横坐标是
,Q点横坐标是 ,M在Q点左边,则M点横坐标为
,M在Q点左边,则M点横坐标为 -4
-4 =-3
=-3 ,代入抛物线解析式可求M点坐标.
,代入抛物线解析式可求M点坐标.
解答:解:(1)∵OA= ,AB=AC=2
,AB=AC=2 ,
,
∴B(- ,0),C(3
,0),C(3 ,0),连接AD,
,0),连接AD,
在Rt△AOD中,AD=2 ,OA=
,OA= ,
,
∴OD= =3,
=3,
∴D的坐标为(0,-3),(3分)
又∵D,C两点在抛物线上,
∴ ,
,
解得 ,
,
∴抛物线的解析式为:y= x2-
x2- x-3,(5分)
x-3,(5分)
当x=- 时,y=0,
时,y=0,
∴点B(-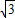 ,0)在抛物线上,(6分)
,0)在抛物线上,(6分)
(2)∵y= x2-
x2- x-3,
x-3,
= (x-
(x-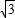 )2-4,
)2-4,
∴抛物线y= x2-
x2- x-3的对称轴方程为x=
x-3的对称轴方程为x= ,(7分)
,(7分)
在抛物线的对称轴上存在点P,使△PBD的周长最小.
∵BD的长为定值∴要使△PBD周长最小只需PB+PD最小.
连接DC,则DC与对称轴的交点即为使△PBD周长最小的点.
设直线DC的解析式为y=mx+n.
由 ,
,
得 ,
,
∴直线DC的解析式为y= x-3.
x-3.
由 ,
,
得 ,
,
故点P的坐标为 .(9分)
.(9分)

(3)存在,设Q( ,t)为抛物线对称轴x=
,t)为抛物线对称轴x= 上一点,
上一点,
M在抛物线上要使四边形BCQM为平行四边形,
则BC∥QM且BC=QM,点M在对称轴的左侧.
于是,过点Q作直线L∥BC与抛物线交于点M(xm,t),
由BC=QM得QM=4 ,
,
从而xm=-3 ,t=12,
,t=12,
另外:M在抛物线的顶点上也可以构造平行四边形!
故在抛物线上存在点M(-3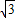 ,12)或(5
,12)或(5 ,12)或(
,12)或( ,-4),使得四边形BCQM为平行四边形.(12分)
,-4),使得四边形BCQM为平行四边形.(12分)
点评:本题考查了点的坐标及二次函数解析式的求法,要求会在坐标系中求线段和最小的问题以及探求平行四边形的条件.
 ,0),B(-
,0),B(- ,0)可求圆半径是2
,0)可求圆半径是2 ,连接AD,在Rt△AOD中,可求OD,即D(0,-3),把C,D两点坐标代入抛物线y=
,连接AD,在Rt△AOD中,可求OD,即D(0,-3),把C,D两点坐标代入抛物线y= x2+bx+c,可求抛物线解析式,将B点坐标代入解析式进行检验即可;
x2+bx+c,可求抛物线解析式,将B点坐标代入解析式进行检验即可;(2)由(1)知,点B关于抛物线对称轴的对称点为点C,连接CD,交抛物线对称轴于P点,P点即为所求,先求直线CD的解析式,已知P点横坐标x=
 ,代入直线CD的解析式即可求P;
,代入直线CD的解析式即可求P;(3)∵BC=4
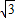 ,Q点横坐标是
,Q点横坐标是 ,M在Q点左边,则M点横坐标为
,M在Q点左边,则M点横坐标为 -4
-4 =-3
=-3 ,代入抛物线解析式可求M点坐标.
,代入抛物线解析式可求M点坐标.解答:解:(1)∵OA=
 ,AB=AC=2
,AB=AC=2 ,
,∴B(-
 ,0),C(3
,0),C(3 ,0),连接AD,
,0),连接AD,
在Rt△AOD中,AD=2
 ,OA=
,OA= ,
,∴OD=
 =3,
=3,∴D的坐标为(0,-3),(3分)
又∵D,C两点在抛物线上,
∴
 ,
,解得
 ,
,∴抛物线的解析式为:y=
 x2-
x2- x-3,(5分)
x-3,(5分)当x=-
 时,y=0,
时,y=0,∴点B(-
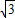 ,0)在抛物线上,(6分)
,0)在抛物线上,(6分)(2)∵y=
 x2-
x2- x-3,
x-3,=
 (x-
(x-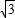 )2-4,
)2-4,∴抛物线y=
 x2-
x2- x-3的对称轴方程为x=
x-3的对称轴方程为x= ,(7分)
,(7分)在抛物线的对称轴上存在点P,使△PBD的周长最小.

∵BD的长为定值∴要使△PBD周长最小只需PB+PD最小.
连接DC,则DC与对称轴的交点即为使△PBD周长最小的点.
设直线DC的解析式为y=mx+n.
由
 ,
,得
 ,
,∴直线DC的解析式为y=
 x-3.
x-3.由
 ,
,得
 ,
,故点P的坐标为
 .(9分)
.(9分)
(3)存在,设Q(
 ,t)为抛物线对称轴x=
,t)为抛物线对称轴x= 上一点,
上一点,M在抛物线上要使四边形BCQM为平行四边形,
则BC∥QM且BC=QM,点M在对称轴的左侧.
于是,过点Q作直线L∥BC与抛物线交于点M(xm,t),
由BC=QM得QM=4
 ,
,从而xm=-3
 ,t=12,
,t=12,另外:M在抛物线的顶点上也可以构造平行四边形!
故在抛物线上存在点M(-3
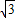 ,12)或(5
,12)或(5 ,12)或(
,12)或( ,-4),使得四边形BCQM为平行四边形.(12分)
,-4),使得四边形BCQM为平行四边形.(12分)点评:本题考查了点的坐标及二次函数解析式的求法,要求会在坐标系中求线段和最小的问题以及探求平行四边形的条件.

练习册系列答案
相关题目
 ,0),B(-
,0),B(- ,0),以点A为圆心,AB为半径的圆与x轴相交于点B,C,与y轴相交于点D,E.
,0),以点A为圆心,AB为半径的圆与x轴相交于点B,C,与y轴相交于点D,E. x2+bx+c经过C,D两点,求抛物线的解析式,并判断点B是否在该抛物线上;
x2+bx+c经过C,D两点,求抛物线的解析式,并判断点B是否在该抛物线上;
 ,0),B(-
,0),B(-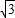 ,0),以点A为圆心,AB为半径的圆与x轴相交于点B,C,与y轴相交于点D,E.
,0),以点A为圆心,AB为半径的圆与x轴相交于点B,C,与y轴相交于点D,E. x2+bx+c经过C,D两点,求抛物线的解析式,并判断点B是否在该抛物线上;
x2+bx+c经过C,D两点,求抛物线的解析式,并判断点B是否在该抛物线上;
 与⊙O的位置关系是( )
与⊙O的位置关系是( )
