题目内容
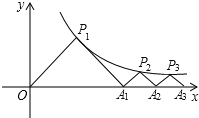
【题目】如图,△P1OA1,△P2A1A2,△P3A2A3,…,△PnAn﹣1An都是等腰直角三角形,点P1,P2,P3,…,Pn在函数y=![]() (x>0)的图象上,斜边OA1,A1A2,A2A3,…,An﹣1An都在x轴上,则点A1的坐标是 ,点A2016的坐标是 .
(x>0)的图象上,斜边OA1,A1A2,A2A3,…,An﹣1An都在x轴上,则点A1的坐标是 ,点A2016的坐标是 .
【答案】(2,0),(24![]() ,0).
,0).
【解析】
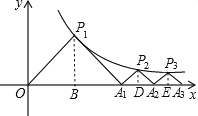
试题分析:分别作出点P1,P2,P3与x轴的垂线段,根据等腰直角三角形三线合一的性质可知,这此垂线段又是斜边上的中线,则等于斜边的一半;设未知数,根据反比例函数关系式列等量关系,求出未知数的值,并取舍,找出规律,并化简.
解:过点P1作P1B⊥x轴于B,
∵△P1OA1是等腰直角三角形,
∴OB=P1B,
则OBP1B=1,
∴OB=1,OA1=2,
∴A1(2,0);
过点P2作P2D⊥x轴于D,设A1D=x,则OD=2+x,
同理得:A1D=P2D=x,
则ODP2D=1,
x(2+x)=1,
解得:x1=﹣1+![]() ,x2=﹣1﹣
,x2=﹣1﹣![]() (舍),
(舍),
∴A2(2![]() ,0)
,0)
过点P3作P3E⊥x轴于E,设P3E=y,则OE=2![]() +y,
+y,
则OEP3E=1,
y(2![]() +y)=1,
+y)=1,
解得:y1=![]() ﹣
﹣![]() ,y2=﹣
,y2=﹣![]() (舍),
(舍),
∴A2A3=2![]() ﹣2
﹣2![]() ,
,
∴OA3=2![]() ﹣2
﹣2![]() +2
+2![]() =2
=2![]() ,
,
∴A3(2![]() ,0),
,0),
所以可以得出:A2016的坐标(2![]() ,0),即(24
,0),即(24![]() ,0),
,0),
故答案为:(2,0),(24![]() ,0).
,0).

练习册系列答案
相关题目
【题目】从某玉米种子中抽取6批,在同一条件下进行发芽试验,有关数据如下:
种子粒数 | 100 | 400 | 800 | 1000 | 2000 | 5000 |
发芽种子粒数 | 85 | 318 | 652 | 793 | 1604 | 4005 |
发芽频率 | 0.850 | 0.795 | 0.815 | 0.793 | 0.802 | 0.801 |
根据以上数据可以估计,该玉米种子发芽的概率约为(精确到0.10).