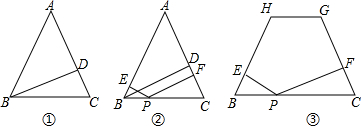
题目内容
已知等腰梯形中,AB=DC=2,AD∥BC,AD=3,腰与底相交所成的锐 角为60°,动点P在线段BC上运动( 点P不与B、C点重合),并且∠APQ=60°,PQ交射线CD于点Q,若CQ=y,BP=x,
角为60°,动点P在线段BC上运动( 点P不与B、C点重合),并且∠APQ=60°,PQ交射线CD于点Q,若CQ=y,BP=x,
(1)求下底BC的长.
(2)求y与x的函数解析式,并指出当点P运动到何位置时,线段CQ最长,最大值为多少?
(3)在(2)的条件下,当CQ最长时,PQ与AD交于点E,求QE的长.
 角为60°,动点P在线段BC上运动( 点P不与B、C点重合),并且∠APQ=60°,PQ交射线CD于点Q,若CQ=y,BP=x,
角为60°,动点P在线段BC上运动( 点P不与B、C点重合),并且∠APQ=60°,PQ交射线CD于点Q,若CQ=y,BP=x,(1)求下底BC的长.
(2)求y与x的函数解析式,并指出当点P运动到何位置时,线段CQ最长,最大值为多少?
(3)在(2)的条件下,当CQ最长时,PQ与AD交于点E,求QE的长.
分析:(1)过点D作DE∥AB,交BC于E,得到?ABED和等边△DEC,则BC=BE+EC=5;
(2)根据两角对应相等的两三角形相似证明出△CPQ∽△BAP,由相似三角形对应边成比例得到CQ:BP=CP:BA,则y=-
x2+
x,根据二次函数的性质可得当x=
,即当点P运动到BC中点时,线段CQ有最大值
;
(3)在(2)的条件下,当CQ最长时,BP=CP=
,CQ=
,则QD=
.先由DE∥CP,得出△QDE∽△QCP,根据相似三角形的性质列出比例式,求出DE=
,并且得出QE:QP=9:25,那么可设QE=9k,QP=25k.再根据两角对应相等的两三角形相似证明△DEQ∽△PEA,DE:PE=EQ:EA,根据相似三角形的对应边成比例得出
:16k=9k:
,解方程求出k=
,进而得到QE的长度.
(2)根据两角对应相等的两三角形相似证明出△CPQ∽△BAP,由相似三角形对应边成比例得到CQ:BP=CP:BA,则y=-
| 1 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| 25 |
| 8 |
(3)在(2)的条件下,当CQ最长时,BP=CP=
| 5 |
| 2 |
| 25 |
| 8 |
| 9 |
| 8 |
| 9 |
| 10 |
| 9 |
| 10 |
| 21 |
| 10 |
| ||
| 40 |
解答: 解:(1)如图1,过点D作DE∥AB,交BC于E,
解:(1)如图1,过点D作DE∥AB,交BC于E,
∵AD∥BC,
∴四边形ABED是平行四边形,
∴BE=AD=3,DE=AB=DC=2,
∵DE∥AB,
∴∠DEC=∠B=60°,
∴△DEC为等边三角形,
∴EC=DC=2,
∴BC=BE+EC=3+2=5;
 (2)如图2,在△CPQ与△BAP中,
(2)如图2,在△CPQ与△BAP中,
∵
,
∴△CPQ∽△BAP,
∴CQ:BP=CP:BA,即y:x=(5-x):2,
∴y=-
x2+
x,
当x=
=
,即当点P运动到BC中点时,线段CQ最长,
此时最大值为
=
;
 (3)如图3,在(2)的条件下,当CQ最长时,BP=CP=
(3)如图3,在(2)的条件下,当CQ最长时,BP=CP=
,CQ=
,
∴QD=CQ-CD=
-2=
.
∵DE∥CP,
∴△QDE∽△QCP,
∴QE:QP=DE:CP=QD:QC,
即QE:QP=DE:
=
:
=9:25,
∴可设QE=9k,QP=25k,且DE=
,
∴PE=QP-QE=16k,AE=AD-DE=3-
=
.
在△DEQ与△PEA中,
∵
,
∴△DEQ∽△PEA,
∴DE:PE=EQ:EA,
∴
:16k=9k:
,
解得k=
,
∴QE=9k=
.
 解:(1)如图1,过点D作DE∥AB,交BC于E,
解:(1)如图1,过点D作DE∥AB,交BC于E,∵AD∥BC,
∴四边形ABED是平行四边形,
∴BE=AD=3,DE=AB=DC=2,
∵DE∥AB,
∴∠DEC=∠B=60°,
∴△DEC为等边三角形,
∴EC=DC=2,
∴BC=BE+EC=3+2=5;
 (2)如图2,在△CPQ与△BAP中,
(2)如图2,在△CPQ与△BAP中,∵
|
∴△CPQ∽△BAP,
∴CQ:BP=CP:BA,即y:x=(5-x):2,
∴y=-
| 1 |
| 2 |
| 5 |
| 2 |
当x=
-
| ||
2×(-
|
| 5 |
| 2 |
此时最大值为
0-(
| ||
4×(-
|
| 25 |
| 8 |
 (3)如图3,在(2)的条件下,当CQ最长时,BP=CP=
(3)如图3,在(2)的条件下,当CQ最长时,BP=CP=| 5 |
| 2 |
| 25 |
| 8 |
∴QD=CQ-CD=
| 25 |
| 8 |
| 9 |
| 8 |
∵DE∥CP,
∴△QDE∽△QCP,
∴QE:QP=DE:CP=QD:QC,
即QE:QP=DE:
| 5 |
| 2 |
| 9 |
| 8 |
| 25 |
| 8 |
∴可设QE=9k,QP=25k,且DE=
| 9 |
| 10 |
∴PE=QP-QE=16k,AE=AD-DE=3-
| 9 |
| 10 |
| 21 |
| 10 |
在△DEQ与△PEA中,
∵
|
∴△DEQ∽△PEA,
∴DE:PE=EQ:EA,
∴
| 9 |
| 10 |
| 21 |
| 10 |
解得k=
| ||
| 40 |
∴QE=9k=
9
| ||
| 40 |
点评:本题考查了等腰梯形的性质,相似三角形的判定与性质,二次函数的性质,综合性较强,有一定难度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
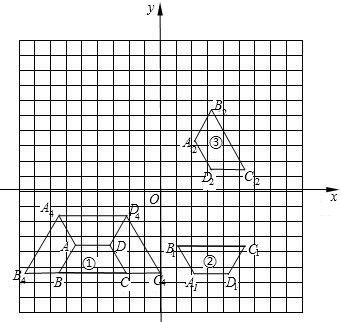 平移8个单位,得到图③;以y轴为对称轴作图③的对称图形,得到等腰梯形A3B3C3D3,即为图④.
平移8个单位,得到图③;以y轴为对称轴作图③的对称图形,得到等腰梯形A3B3C3D3,即为图④.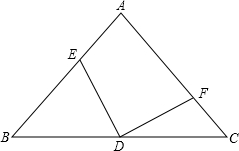 已知等腰△ABC中,AB=AC,D是BC的中点,将三角板中的90°角的顶点绕D点在△ABC内旋转,角的两边分别与AB、AC交于E、F,且点E、F不与A、B、C三点重合.
已知等腰△ABC中,AB=AC,D是BC的中点,将三角板中的90°角的顶点绕D点在△ABC内旋转,角的两边分别与AB、AC交于E、F,且点E、F不与A、B、C三点重合.