题目内容
18．
如图，PA、PB分别切⊙O于点A、B，点E是⊙O上一点，且∠AEB=60°，则∠P=（ ）| A． | 90° | B． | 60° | C． | 45° | D． | 30° |
分析 连接OA，BO，由圆周角定理知可知∠AOB=2∠E=120°，PA、PB分别切⊙O于点A、B，利用切线的性质可知∠OAP=∠OBP=90°，根据四边形内角和可求得∠P=180°-∠AOB=60°．
解答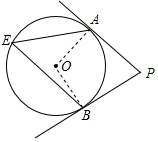 
解：连接OA，BO；
∵∠AOB=2∠E=120°，
∴∠OAP=∠OBP=90°，
∴∠P=180°-∠AOB=60°．
故选B．
点评 本题考查了切线的性质，利用了圆周角定理，切线的性质，四边形的内角和为360度求解，连接OA，OB构造垂直是解题关键．
练习册系列答案
相关题目
8．关于x的方程kx2-4x+3=0与x轴有交点，则k的范围是（ ）
| A． | k＜$\frac{4}{3}$ | B． | k＜$\frac{4}{3}$且k≠0 | C． | k≤$\frac{4}{3}$ | D． | k≤$\frac{4}{3}$且k≠0 |
如图，形如量角器的半圆O的直径DE=12cm，形如三角板的△ABC中，∠ACB=90°，∠ABC=30°，BC=12cm半圆O以2cm/s的速度从左向右运动，在运动过程中，点D、E始终在直线BC上．设运动时间为t（s），当t=0s时，半圆O在△ABC的左侧，OC=8cm．
6．下列计算正确的是（ ）
| A． | 2$\sqrt{2}$+4$\sqrt{3}$=6$\sqrt{5}$ | B． | 3$\sqrt{2}$-2$\sqrt{2}$=1 | C． | $\sqrt{24}$÷$\sqrt{6}$=4 | D． | $\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$ |
13．
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论：
（1）a，b同号；
（2）b2-4ac＞0；
（3）4a+b+c＞0；
（4）当y=-2时，x的值只能取0；
（5）当x=1和x=3时，函数值相等．
其中正确的个数是（ ）
已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，则下列结论：（1）a，b同号；
（2）b2-4ac＞0；
（3）4a+b+c＞0；
（4）当y=-2时，x的值只能取0；
（5）当x=1和x=3时，函数值相等．
其中正确的个数是（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
7．方程x2=2x的根是（ ）
| A． | 0 | B． | 2 | C． | 0或2 | D． | 无解 |