题目内容

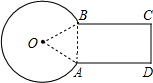如图，一种零件的横截面由三角形、矩形、扇形组成，其中∠BOA=60°，AD=25mm，半径AO=10mm，求该零件的横截面积．

解：∵OB=OA，∠BOA=60°，
∴△BOA是等边三角形；
∴OB=OA=AB=10mm；
过点O作OE⊥AB于点E，
∴∠BOE= $\text{[math]}$ ∠BOA= $\text{[math]}$ ×60°=30°；
又∵AO=10mm（已知），
∴OE=OBcos30°=5 $\text{[math]}$ mm，
∴S_横截面=S_矩形ABCD+S_△BOA+S_扇形BOA=AD•OB+ $\text{[math]}$ AB•OE+ $\text{[math]}$ =25mm×10mm+ $\text{[math]}$ ×10mm×5 $\text{[math]}$ mm+ $\text{[math]}$ =250+25 $\text{[math]}$ + $\text{[math]}$ （mm²）．
分析：根据S_横截面=S_矩形ABCD+S_△BOA+S_扇形BOA，分别计算矩形的长、宽，等边△BOA的底、高，扇形BOA的半径，弧度数，再根据面积公式分别计算．
点评：本题综合考查了扇形面积的计算、矩形的性质以及等边三角形的判定与性质．本题采用了“割补法”，分别求得三角形、矩形以及扇形的面积，然后再求和．