Question

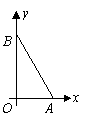
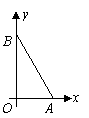
已知一个直角三角形纸片，其中．如图，将该纸片放置在平面直角坐标系中，折叠该纸片，折痕与边交于点，与边交于点．

（1）若折叠后使点与点重合，求点的坐标；

（2）若折叠后点落在边上的点为，设，，试写出关于的函数解析式，并确定的取值范围；

（3）若折叠后点落在边上的点为，且使，求此时点的坐标．

Answer 1

本小题满分12分.

解（1）如图①，折叠后点与点重合，

则

设点的坐标为.

则.

于是.

在中，由勾股定理，得，

即，解得.

点的坐标为.

（2）如图②，折叠后点落在边上的点为,

则.

由题设，

则，

在中，由勾股定理，得.

，

即

由点在边上，有，

解析式为所求.

当时，随的增大而减小，

的取值范围为.

（3）如图③，折叠后点落在边上的点为，且.

则.

又，有.

.

有，得. 

在中，

设，则.

由（2）的结论，得，

解得.

点的坐标为.