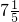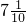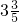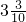题目内容
一个三角形三边的长分别是9,12,15,这个三角形最长边上的高是( )
分析:首先由一个三角形三边的长分别是9,12,15,根据勾股定理的逆定理,可判定此三角形是直角三角形,然后利用三角形的面积,可求得这个三角形最长边上的高.
解答:解:∵一个三角形三边的长分别是9,12,15,
又∵152=225,92+122=81+144=225,
∴152=92+122,
∴这个三角形是直角三角形,
∴这个三角形最长边上的高是:
=
=7
.
故选A.
又∵152=225,92+122=81+144=225,
∴152=92+122,
∴这个三角形是直角三角形,
∴这个三角形最长边上的高是:
| 9×12 |
| 15 |
| 36 |
| 5 |
| 1 |
| 5 |
故选A.
点评:此题考查了勾股定理的逆定理.此题难度适中,注意掌握勾股定理的逆定理:如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
 cm、
cm、 cm、
cm、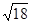 cm,则它的周长为 cm。
cm,则它的周长为 cm。 cm、
cm、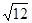 cm、
cm、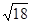 cm,则它的周长为
cm。
cm,则它的周长为
cm。