题目内容
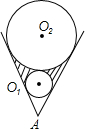 在一个V字形支架上摆放了两种口径不同的试管,如图,是它的轴截面,已知⊙O1的半径是1,⊙O2的半径是3,则图中阴影部分的面积是( )
在一个V字形支架上摆放了两种口径不同的试管,如图,是它的轴截面,已知⊙O1的半径是1,⊙O2的半径是3,则图中阴影部分的面积是( )A、8
| ||||
B、4
| ||||
C、4
| ||||
D、8
|
分析:连接圆心,连接圆心和切点,作O1E⊥O2B于点E,利用勾股定理可得O1E的长度及∠O1O2B,∠O2O1C的度数,那么阴影部分的面积=2×(直角梯形的面积-S扇形BO2O1-S扇形CO1O2).
解答: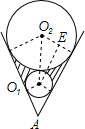 解:连接O1C,O2B,作O1E⊥O2B于点E,
解:连接O1C,O2B,作O1E⊥O2B于点E,
∵O1O2=4,EO2=3-1=2,
∴EO1=2
,
∴∠BO2O1=60°,
∴∠CO1O2=120°,
∴S阴影=2×[
×(1+3)×2
-
-
]=8
-
π.
故选D.
 解:连接O1C,O2B,作O1E⊥O2B于点E,
解:连接O1C,O2B,作O1E⊥O2B于点E,∵O1O2=4,EO2=3-1=2,
∴EO1=2
| 3 |
∴∠BO2O1=60°,
∴∠CO1O2=120°,
∴S阴影=2×[
| 1 |
| 2 |
| 3 |
| 60π×32 |
| 360 |
| 120π×12 |
| 360 |
| 3 |
| 11 |
| 3 |
故选D.
点评:考查两圆相切问题的有关计算;得到阴影部分的组成是解决本题的关键;注意连接圆心,及圆心与切点等常用辅助线作法的应用.

练习册系列答案
相关题目



 -
- π
π



 -
- π
π



 -
- π
π



 -
- π
π