题目内容
【题目】已知:A(0,1)、B(2,0),C(4,3),
(1)在直角坐标系中画出△ABC;
(2)求△ABC的面积;
(3)设点P在x轴上,且△ABP与△ABC的面积相等,请直接写出点P的坐标.
【答案】(1)画图见解析;(2)4;(3)p(10;0),(-6;0)
【解析】试题分析:(1)确定出点A、B、C的位置,连接AC、CB、AB即可;(2)过点C向x、y轴作垂线,垂足为D、E,△ABC的面积=四边形DOEC的面积-△ACE的面积-△BCD的面积-△AOB的面积;(3)因为点p在x轴上,由△ABP的面积=4,求得:BP=8,故此点P的坐标为(10,0)或(-6,0).
试题解析:(1)如图所示:
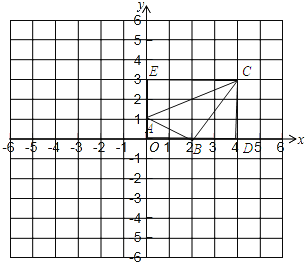
(2)过点C向x、y轴作垂线,垂足为D. E.
∴四边形DOEC的面积=3×4=12,△BCD的面积=![]() ×2×3=3,△ACE的面积=
×2×3=3,△ACE的面积=![]() ×2×4=4,△AOB的面积=
×2×4=4,△AOB的面积=![]() ×2×1=1.
×2×1=1.
∴△ABC的面积=四边形DOEC的面积△ACE的面积△BCD的面积△AOB的面积
=12341=4.
(3)因为点p在x轴上,
所以△ABP的面积=![]() AOBP=4,即:
AOBP=4,即:![]() ×1×BP=4,解得:BP=8,
×1×BP=4,解得:BP=8,
所点P的坐标为(10,0)或(6,0);
当点P在y轴上时,△ABP的面积=12×BO×AP=4,即12×2×AP=4,解得:AP=4.

练习册系列答案
相关题目