题目内容
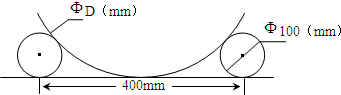
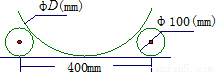
如图在平台上用直径为100mm的两根圆钢棒嵌在大型工件的两侧,测量大的圆形工件的直径D,测得两根圆钢棒外侧距离为400mm,则工件直径D(mm)用科学记数法可写为
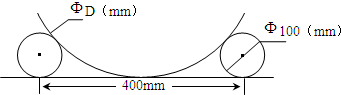
- A.2×102
- B.200
- C.0.4×103
- D.4×102
D
分析:首先根据题意找到大圆的圆心,然后求得OC,OE与EC的长,利用勾股定理列方程,即可求得答案.
解答: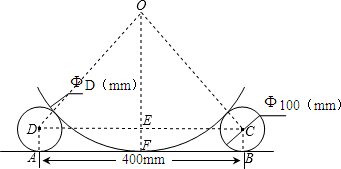 解:如图,点O是大的圆形工件的圆心,连接OC,OD,CD,BC,AD.
解:如图,点O是大的圆形工件的圆心,连接OC,OD,CD,BC,AD.
∵⊙O与⊙C相切,⊙O与⊙D相切,AB是⊙O的切线,
∴∠DAB=∠ABC=90°∠ADE=90°,
∴AD∥BC,
∵AD=BC,
∴四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
∴CD=AB=400mm,
∵OF⊥CD,
∵OD=OC,
∴CE=200mm,
设大的圆形工件的半径为x,OC=x+50,则OE=x-50(mm),
∵OC2=OE2+EC2,
即(x+50)2=(x-50)2+40000,
解得:x=200,
∴大的圆形工件的直径为400mm,
用科学记数法可写为:4×102.
故选D.
点评:此题考查了圆与圆的位置关系,切线的性质以及直角三角形的性质等知识.此题综合性较强,难度适中,解题的关键是方程思想与数形结合思想的应用.
分析:首先根据题意找到大圆的圆心,然后求得OC,OE与EC的长,利用勾股定理列方程,即可求得答案.
解答:
 解:如图,点O是大的圆形工件的圆心,连接OC,OD,CD,BC,AD.
解:如图,点O是大的圆形工件的圆心,连接OC,OD,CD,BC,AD.∵⊙O与⊙C相切,⊙O与⊙D相切,AB是⊙O的切线,
∴∠DAB=∠ABC=90°∠ADE=90°,
∴AD∥BC,
∵AD=BC,
∴四边形ABCD是平行四边形,
∴四边形ABCD是矩形,
∴CD=AB=400mm,
∵OF⊥CD,
∵OD=OC,
∴CE=200mm,
设大的圆形工件的半径为x,OC=x+50,则OE=x-50(mm),
∵OC2=OE2+EC2,
即(x+50)2=(x-50)2+40000,
解得:x=200,
∴大的圆形工件的直径为400mm,
用科学记数法可写为:4×102.
故选D.
点评:此题考查了圆与圆的位置关系,切线的性质以及直角三角形的性质等知识.此题综合性较强,难度适中,解题的关键是方程思想与数形结合思想的应用.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
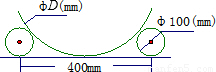
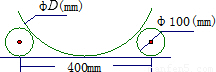
如图在平台上用直径为100mm的两根圆钢棒嵌在大型工件的两侧,测量大的圆形工件的直径D,测得两根圆钢棒与地的两个接触点之间的距离为400mm,则工件直径D(mm)用科学记数法可表示为( )mm.


| A、4×104 | B、0.4×105 | C、20000 | D、4×102 |