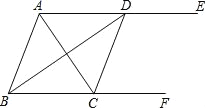
题目内容
【题目】如图,在 ![]() 中,
中,![]() ,F是 AB 延长线上一点,
,F是 AB 延长线上一点,![]() ,
,![]() 于点 D,交 BC 于点E.
于点 D,交 BC 于点E.
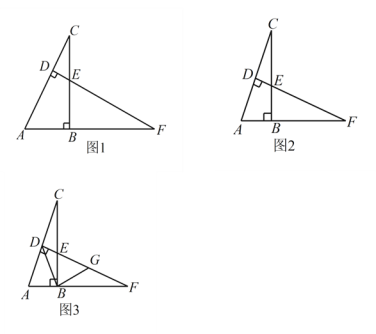
(1)如图1,求证:![]() ;
;
(2)如图2,若点 ![]() 是
是 ![]() 边的中点,求
边的中点,求 ![]() 的度数;
的度数;
(3)如图3,在(2)的条件下,连接 ![]() ,作
,作 ![]() ,交
,交 ![]() 于点G,若
于点G,若 ![]() ,
,![]() .求
.求 ![]() 的面积
的面积
【答案】(1)详见解析;(2)67.5°;(3)![]() .
.
【解析】
(1)先证明三角形全等,利用全等性质即可解出此题
(2)连接CF,得出等腰Rt△BCF,由此得出角度关系,根据D又是中点DF⊥AC可以得出△AFC为等腰三角形,则DF就为角平分线,因此可以得出角度关系,联合求解即可.
(3)先证出△BCD≌△BFG,再证出△ABC≌△EBF,从而得出BEG和BEF的关系即可.
(1)证明:
∵FD⊥AC
∴∠ADF=90°
∵∠ABC=90°
∴∠ADF=∠ABC=∠EBF
∵∠C+∠A=∠F+∠A=90°
∴∠C=∠F
在△ABC和△EBF中
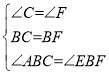
∴△ABC≌△EBF
∴AC=EF
(2)
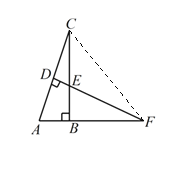
连接CF
∵点D是AC中点
∴AD=CD
∵FD⊥AC
∴∠ADF=∠CDF=90°
在△ADF和△CDF中
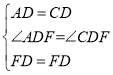
∴△ADF≌△CDF
∴∠AFD=∠CFD
∵BF=BC,BC⊥BF
∴△BCF是等腰直角三角形
∴∠BFC=∠BCF=∠AFD+∠CFD=45°
∴∠AFD=∠CFD=22.5°
∴∠A=90°-∠AFD=90°-22.5°=67.5°
(3)∵BG⊥BD
∴∠DBG=90°
∴∠DBC+∠EBG=∠FBG+∠EBG=90°
∴∠DBC=∠FBG
在△BCD和△BFG中
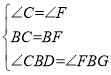
∴△BCD≌△BFG
∴CD=FG
∵CD=AD,AC=EF
∴FG=EG
∵△ABC≌△EBF
∴AB=BE=1
∴BF=BC=BE+CE=1+![]()
∴![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目