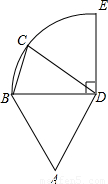
题目内容
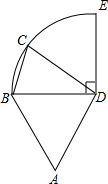 如图,
如图, |
| BE |
| 1 |
| 4 |
 |
| BE |
分析:四边形ABCD的周长P就是四边形的四边的和,四边中AB,AD,CD的长是BD长度确定,因而本题就是确定BC的范围,BC一定大于0,且小于或等于BE,只要求出BE的长就可以.
解答:解:∵△ABD是等边三角形,
∴AB+AD+CD=18,得p>18,
∵BC的最大值为当点C与E重合的时刻,BE=6
,
∴p≤18+6
,
∴p的取值范围是18<P≤18+6
.
故答案为:18<P≤18+6
.
∴AB+AD+CD=18,得p>18,
∵BC的最大值为当点C与E重合的时刻,BE=6
| 2 |
∴p≤18+6
| 2 |
∴p的取值范围是18<P≤18+6
| 2 |
故答案为:18<P≤18+6
| 2 |
点评:此题考查了圆的性质与直角三角形的性质.解题的关键是找到临界点,将动态问题转化为普通的几何计算问题.注意数形结合思想的应用.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 圆周,C点是
圆周,C点是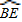 上的任意一点,△ABD是等边三角形,则四边形ABCD的周长P的取值范围是( )
上的任意一点,△ABD是等边三角形,则四边形ABCD的周长P的取值范围是( )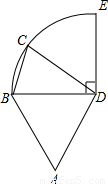
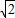
 圆周,C点是
圆周,C点是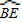 上的任意一点,△ABD是等边三角形,则四边形ABCD的周长P的取值范围是( )
上的任意一点,△ABD是等边三角形,则四边形ABCD的周长P的取值范围是( )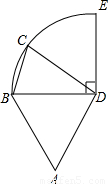
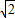
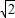
 圆周,C点是
圆周,C点是 上的任意一点,△ABD是等边三角形,则四边形ABCD的周长P的取值范围是( )
上的任意一点,△ABD是等边三角形,则四边形ABCD的周长P的取值范围是( )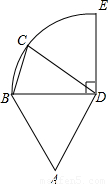
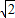
 圆周,C点是
圆周,C点是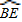 上的任意一点,△ABD是等边三角形,则四边形ABCD的周长P的取值范围是( )
上的任意一点,△ABD是等边三角形,则四边形ABCD的周长P的取值范围是( )