题目内容
已知在锐角△ABC中，∠A=50°，AB＞BC．则∠B的取值范围是
- A.30°＜∠B＜50°
- B.40°＜∠B＜60°
- C.40°＜∠B＜80°
- D.50°＜∠B＜100°
C
分析：当BC最短时，∠B一定大于当AB是斜边时，∠B的度数，∠B的度数一定小于当AB=BC时，∠B的度数．据此即可求解．
解答：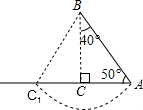
解：如图，当BC最短时，∠ABC=40°，
现以B为圆心，AB长为半径画弧交直线AC于点C1，
当BC1的长等于AB时，∠ABC1=80°，
所以40°＜∠B＜80°．
故选C．
点评：本题主要考查了三角形的边角关系，正确理解∠B的范围的确定方法是解决本题的关键．
分析：当BC最短时，∠B一定大于当AB是斜边时，∠B的度数，∠B的度数一定小于当AB=BC时，∠B的度数．据此即可求解．
解答：
解：如图，当BC最短时，∠ABC=40°，现以B为圆心，AB长为半径画弧交直线AC于点C1，
当BC1的长等于AB时，∠ABC1=80°，
所以40°＜∠B＜80°．
故选C．
点评：本题主要考查了三角形的边角关系，正确理解∠B的范围的确定方法是解决本题的关键．
练习册系列答案
学练快车道口算心算速算天天练系列答案
相关题目
29、如图，已知在锐角△ABC中，∠ABC=2∠C，∠ABC的平分线与AD垂直于D，求证：AC=2BD．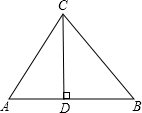
在锐角△ABC中，∠A，∠B，∠C的对边分别是a，b，c．如图所示，过C作CD⊥AB，垂足为点D，则cosA=
已知在锐角△ABC中，I是△ABC三条角平分线的交点，IG⊥BC于G，试比较∠1与∠2的大小，并说明理由．
如图，已知在锐角△ABC中，∠ABC=2∠C，∠ABC的平分线与AD垂直于D，求证：AC=2BD．