题目内容
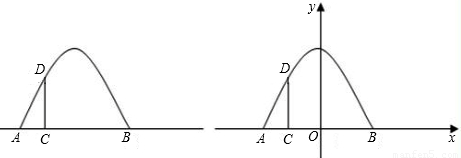
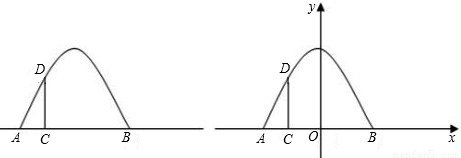
 如图所示,某建筑物有一抛物线形的大门,小强想知道这道门的高度,他先测出门的宽度AB=8m,然后用一根长为4m的小竹竿CD竖直的接触地面和门的内壁,并测得AC=1m,则门高OE为
如图所示,某建筑物有一抛物线形的大门,小强想知道这道门的高度,他先测出门的宽度AB=8m,然后用一根长为4m的小竹竿CD竖直的接触地面和门的内壁,并测得AC=1m,则门高OE为
- A.9m
- B.

- C.8.7m
- D.9.3m
B
分析:根据所建坐标系,易求A、B、D的坐标,因它们都在抛物线上,所以代入解析式得方程组求解,再求顶点坐标得高度OE长.
解答:由题意得,抛物线过点A(-4,0)、B(4,0)、D(-3,4),
设y=a(x+4)(x-4),
把D(-3,4)代入y=a(x+4)(x-4),
得4=a(-3+4)(-3-4),
解得a=- ,
,
∴y=- (x+4)(x-4).
(x+4)(x-4).
令x=0得y= ,即(0,
,即(0, ),
),
∴OE=
∴门的高度约为 m.
m.
故选:B.
点评:此题主要考查了二次函数的应用,根据所建坐标系及图形特点,选择合适的函数表达式形式,有利于减小计算量.本题选取交点式较简便.
分析:根据所建坐标系,易求A、B、D的坐标,因它们都在抛物线上,所以代入解析式得方程组求解,再求顶点坐标得高度OE长.
解答:由题意得,抛物线过点A(-4,0)、B(4,0)、D(-3,4),
设y=a(x+4)(x-4),
把D(-3,4)代入y=a(x+4)(x-4),
得4=a(-3+4)(-3-4),
解得a=-
 ,
,∴y=-
 (x+4)(x-4).
(x+4)(x-4).令x=0得y=
 ,即(0,
,即(0, ),
),∴OE=

∴门的高度约为
 m.
m.故选:B.
点评:此题主要考查了二次函数的应用,根据所建坐标系及图形特点,选择合适的函数表达式形式,有利于减小计算量.本题选取交点式较简便.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

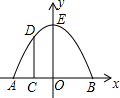 如图所示,某建筑物有一抛物线形的大门,小强想知道这道门的高度,他先测出门的宽度AB=8m,然后用一根长为4m的小竹竿CD竖直的接触地面和门的内壁,并测得AC=1m,则门高OE为( )
如图所示,某建筑物有一抛物线形的大门,小强想知道这道门的高度,他先测出门的宽度AB=8m,然后用一根长为4m的小竹竿CD竖直的接触地面和门的内壁,并测得AC=1m,则门高OE为( )