题目内容
如图,AB是⊙O的直径,AM和BN是它的两条切线,DE切⊙O于点E,交AM于点D,交BN于点C,
(1)求证:OD∥BE;
(2)如果OD=6cm,OC=8cm,求CD的长.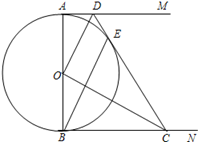
(1)求证:OD∥BE;
(2)如果OD=6cm,OC=8cm,求CD的长.

(1)证明见解析(2)10
解:(1)证明:连接OE,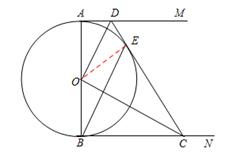
∵AM、DE是⊙O的切线,OA、OE是⊙O的半径,
∴∠ADO=∠EDO, ∠DAO=∠DEO=90°。
∴∠AOD=∠EOD=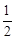 ∠AOE。
∠AOE。
∵∠ABE=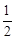 ∠AOE,∴∠AOD=∠ABE。
∠AOE,∴∠AOD=∠ABE。
∴OD∥BE。
(2)由(1)得:∠AOD=∠EOD=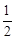 ∠AOE,
∠AOE,
同理,有:∠BOC=∠EOC=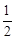 ∠BOE。
∠BOE。
∴∠AOD+∠EOD+∠BOC+∠EOC=180°。∴∠EOD+∠EOC=90°。
∴△DOC是直角三角形。
∵OD=6cm,OC=8cm,
∴ (cm) 。
(cm) 。
(1)首先连接OE,由AM和BN是它的两条切线,易得∠ADO=∠EDO,∠DAO=∠DEO=90°,由切线长定理,可得∠AOD=∠EOD=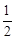 ∠AOE,∠AOD=∠ABE,根据同位角相等,两直线平行,即可证得OD∥BE。
∠AOE,∠AOD=∠ABE,根据同位角相等,两直线平行,即可证得OD∥BE。
(2)由(1),易证得∠EOD+∠EOC=90°,然后利用勾股定理,即可求得CD的长。

∵AM、DE是⊙O的切线,OA、OE是⊙O的半径,
∴∠ADO=∠EDO, ∠DAO=∠DEO=90°。
∴∠AOD=∠EOD=
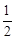 ∠AOE。
∠AOE。 ∵∠ABE=
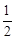 ∠AOE,∴∠AOD=∠ABE。
∠AOE,∴∠AOD=∠ABE。∴OD∥BE。
(2)由(1)得:∠AOD=∠EOD=
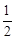 ∠AOE,
∠AOE,同理,有:∠BOC=∠EOC=
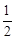 ∠BOE。
∠BOE。∴∠AOD+∠EOD+∠BOC+∠EOC=180°。∴∠EOD+∠EOC=90°。
∴△DOC是直角三角形。
∵OD=6cm,OC=8cm,
∴
 (cm) 。
(cm) 。(1)首先连接OE,由AM和BN是它的两条切线,易得∠ADO=∠EDO,∠DAO=∠DEO=90°,由切线长定理,可得∠AOD=∠EOD=
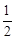 ∠AOE,∠AOD=∠ABE,根据同位角相等,两直线平行,即可证得OD∥BE。
∠AOE,∠AOD=∠ABE,根据同位角相等,两直线平行,即可证得OD∥BE。(2)由(1),易证得∠EOD+∠EOC=90°,然后利用勾股定理,即可求得CD的长。

练习册系列答案
相关题目
 是⊙
是⊙ 的直径,弦
的直径,弦 ,垂足为
,垂足为 ,如果
,如果 ,
, ,那么线段
,那么线段 的长是 .
的长是 .


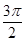
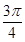
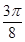
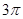
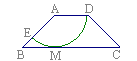
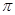 ,则扇形的半径是( )
,则扇形的半径是( )