题目内容
先阅读，后解题：要说明代数式2x2+8x+10的值恒大于0还是恒等于0或者恒小于0，我们可以将它配方成一个平方式加上一个常数的形式，再去考虑，具体过程如下：
解：2x2+8x+10
=2（x2+4x+5）（提公因式，得到一个二次项系数为1的二次多项式）
=2（x2+4x+22-22+5）
=2[（x+2）2+1]（将二次多项式配方）
=2（x+2）2+2 （去掉中括号）
因为当x取任意实数时，代数式2（x+2）2的值一定是非负数，那么2（x+2）2+2的值一定为正数，所以，原式的值恒大于0，并且，当x=-2时，原式有最小值2．请仿照上例，说明代数式-2x2-8x-10的值恒大于0还是恒小于0，并且说明它的最大值或者最小值是什么．
解：2x2+8x+10
=2（x2+4x+5）（提公因式，得到一个二次项系数为1的二次多项式）
=2（x2+4x+22-22+5）
=2[（x+2）2+1]（将二次多项式配方）
=2（x+2）2+2 （去掉中括号）
因为当x取任意实数时，代数式2（x+2）2的值一定是非负数，那么2（x+2）2+2的值一定为正数，所以，原式的值恒大于0，并且，当x=-2时，原式有最小值2．请仿照上例，说明代数式-2x2-8x-10的值恒大于0还是恒小于0，并且说明它的最大值或者最小值是什么．
分析：按照题目提供的方法将二次三项式配方后即可得到答案．
解答：解：-2x2-8x-10
=-2（x2+4x+5）
=-2（x2+4x+22-22+5）
=-2[（x+2）2+1]
=-2（x+2）2-2
因为当x取任意实数时，代数式2（x+2）2的值一定是非负数，那么-2（x+2）2-2的值一定为负数，所以，原式的值恒小于0，并且，当x=-2时，原式有最大值-2．
=-2（x2+4x+5）
=-2（x2+4x+22-22+5）
=-2[（x+2）2+1]
=-2（x+2）2-2
因为当x取任意实数时，代数式2（x+2）2的值一定是非负数，那么-2（x+2）2-2的值一定为负数，所以，原式的值恒小于0，并且，当x=-2时，原式有最大值-2．
点评：此题考查了配方法与完全平方式的非负性的应用．注意解此题的关键是将原代数式准确配方．
练习册系列答案
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
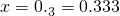…，则10x=3.333…，
10x=3+x9x=3，即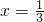
．
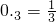．根据上述提供的方法把下列两个循环小数化成分数．
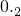； （2）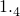
．