题目内容
 已知:反比例函数
已知:反比例函数 和
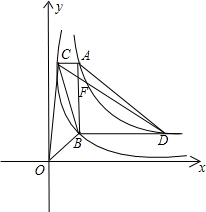
和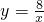 在平面直角坐标系xOy第一象限中的图象如图所示,点A在
在平面直角坐标系xOy第一象限中的图象如图所示,点A在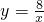 的图象上,AB∥y轴,与
的图象上,AB∥y轴,与 的图象交于点B,AC、BD与x轴平行,分别与
的图象交于点B,AC、BD与x轴平行,分别与 、
、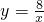 的图象交于点C、D.
的图象交于点C、D.
(1)若点A的横坐标为2,求直线CD的解析式:
(2)若点A的横坐标为m,梯形ACBD的对角线的交点F,求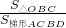 的值.
的值.
解:(1)把x=2代入y= 得y=4,则A点坐标为(2,4),
得y=4,则A点坐标为(2,4),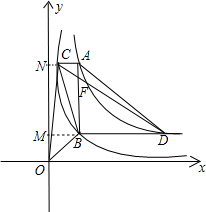
∵AC∥x轴,AB∥y轴,
∵C点的纵坐标为4,B点的横坐标为2,
把y=4代入y= 得x=
得x= ;把x=2代入y=
;把x=2代入y= 得y=1,
得y=1,
∴C点坐标为( ,4),B点坐标为(2,1),
,4),B点坐标为(2,1),
∵BD∥x轴,
∴D点的纵坐标与B的纵坐标相等,
把y=1代入y= 得x=8,
得x=8,
∴D点坐标为(8,1),
设直线DC的解析式为y=kx+b,
把C( ,4)、D(8,1)代入
,4)、D(8,1)代入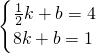 ,解得
,解得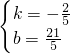 ,
,
∴直线DC的解析式为y=- x+
x+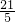 ;
;
(2)作CM⊥y轴于M,BN⊥y轴于N,如图,
当点A的横坐标为m,与(1)的方法一样可确定A点坐标为(m, ),C点坐标为(
),C点坐标为( ,
, ),B点坐标为(m,
),B点坐标为(m, ),D点坐标为(4m,
),D点坐标为(4m, ),
),
∴AC=m- =
= ,BD=4m-m=3m,AB=
,BD=4m-m=3m,AB= -
- =
= ,
,
∴S梯形ACBD= (
( +3m)•
+3m)• =
= ;
;
∵S△OCN=S△OBM= ×2=1,S梯形BMNC=
×2=1,S梯形BMNC= (
( +m)•
+m)• =
= ,
,
而S四边形BONC=S△ONC+S△OBC=S梯形BMNC+S△OBM,
∴S△OBC=S梯形BMNC= ,
,
∴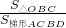 =
=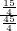 =
= .
.
分析:(1)先利用点A在y= 的图象上可确定A点坐标为(2,4),则根据AC∥x轴,AB∥y轴得到C点的纵坐标为4,B点的横坐标为2,再利用C、B在y=
的图象上可确定A点坐标为(2,4),则根据AC∥x轴,AB∥y轴得到C点的纵坐标为4,B点的横坐标为2,再利用C、B在y= 的图象上可确定C点坐标为(
的图象上可确定C点坐标为( ,4),B点坐标为(2,1);由于BD∥x轴,则D点的纵坐标与B的纵坐标相等,根据D点在y=
,4),B点坐标为(2,1);由于BD∥x轴,则D点的纵坐标与B的纵坐标相等,根据D点在y= 的图象上可确定D点坐标为(8,1),然后利用待定系数法求出直线CD的解析式;
的图象上可确定D点坐标为(8,1),然后利用待定系数法求出直线CD的解析式;
(2)作CM⊥y轴于M,BN⊥y轴于N,与(1)的方法一样可确定A点坐标为(m, ),C点坐标为(
),C点坐标为( ,
, ),B点坐标为(m,
),B点坐标为(m, ),D点坐标为(4m,
),D点坐标为(4m, ),根据比例系数的几何意义得到S△OCN=S△OBM=1,根据梯形的面积公式得到S梯形BMNC=
),根据比例系数的几何意义得到S△OCN=S△OBM=1,根据梯形的面积公式得到S梯形BMNC= ,S梯形ACBD=
,S梯形ACBD= ;再利用S四边形BONC=S△ONC+S△OBC=S梯形BMNC+S△OBM得S△OBC=S梯形BMNC=
;再利用S四边形BONC=S△ONC+S△OBC=S梯形BMNC+S△OBM得S△OBC=S梯形BMNC= ,最后计算
,最后计算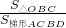 的值.
的值.
点评:本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征、比例系数的几何意义和待定系数法求函数的解析式;记住梯形的面积公式和运用几何图形的面积和差求不规则几何图形的面积.
 得y=4,则A点坐标为(2,4),
得y=4,则A点坐标为(2,4),
∵AC∥x轴,AB∥y轴,
∵C点的纵坐标为4,B点的横坐标为2,
把y=4代入y=
 得x=
得x= ;把x=2代入y=
;把x=2代入y= 得y=1,
得y=1,∴C点坐标为(
 ,4),B点坐标为(2,1),
,4),B点坐标为(2,1),∵BD∥x轴,
∴D点的纵坐标与B的纵坐标相等,
把y=1代入y=
 得x=8,
得x=8,∴D点坐标为(8,1),
设直线DC的解析式为y=kx+b,
把C(
 ,4)、D(8,1)代入
,4)、D(8,1)代入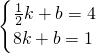 ,解得
,解得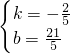 ,
,∴直线DC的解析式为y=-
 x+
x+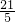 ;
;(2)作CM⊥y轴于M,BN⊥y轴于N,如图,
当点A的横坐标为m,与(1)的方法一样可确定A点坐标为(m,
 ),C点坐标为(
),C点坐标为( ,
, ),B点坐标为(m,
),B点坐标为(m, ),D点坐标为(4m,
),D点坐标为(4m, ),
),∴AC=m-
 =
= ,BD=4m-m=3m,AB=
,BD=4m-m=3m,AB= -
- =
= ,
,∴S梯形ACBD=
 (
( +3m)•
+3m)• =
= ;
;∵S△OCN=S△OBM=
 ×2=1,S梯形BMNC=
×2=1,S梯形BMNC= (
( +m)•
+m)• =
= ,
,而S四边形BONC=S△ONC+S△OBC=S梯形BMNC+S△OBM,
∴S△OBC=S梯形BMNC=
 ,
,∴
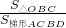 =
=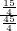 =
= .
.分析:(1)先利用点A在y=
 的图象上可确定A点坐标为(2,4),则根据AC∥x轴,AB∥y轴得到C点的纵坐标为4,B点的横坐标为2,再利用C、B在y=
的图象上可确定A点坐标为(2,4),则根据AC∥x轴,AB∥y轴得到C点的纵坐标为4,B点的横坐标为2,再利用C、B在y= 的图象上可确定C点坐标为(
的图象上可确定C点坐标为( ,4),B点坐标为(2,1);由于BD∥x轴,则D点的纵坐标与B的纵坐标相等,根据D点在y=
,4),B点坐标为(2,1);由于BD∥x轴,则D点的纵坐标与B的纵坐标相等,根据D点在y= 的图象上可确定D点坐标为(8,1),然后利用待定系数法求出直线CD的解析式;
的图象上可确定D点坐标为(8,1),然后利用待定系数法求出直线CD的解析式;(2)作CM⊥y轴于M,BN⊥y轴于N,与(1)的方法一样可确定A点坐标为(m,
 ),C点坐标为(
),C点坐标为( ,
, ),B点坐标为(m,
),B点坐标为(m, ),D点坐标为(4m,
),D点坐标为(4m, ),根据比例系数的几何意义得到S△OCN=S△OBM=1,根据梯形的面积公式得到S梯形BMNC=
),根据比例系数的几何意义得到S△OCN=S△OBM=1,根据梯形的面积公式得到S梯形BMNC= ,S梯形ACBD=
,S梯形ACBD= ;再利用S四边形BONC=S△ONC+S△OBC=S梯形BMNC+S△OBM得S△OBC=S梯形BMNC=
;再利用S四边形BONC=S△ONC+S△OBC=S梯形BMNC+S△OBM得S△OBC=S梯形BMNC= ,最后计算
,最后计算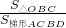 的值.
的值.点评:本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征、比例系数的几何意义和待定系数法求函数的解析式;记住梯形的面积公式和运用几何图形的面积和差求不规则几何图形的面积.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
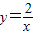 和
和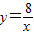 在平面直角坐标系xOy第一象限中的图象如图所示,点A在
在平面直角坐标系xOy第一象限中的图象如图所示,点A在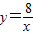 的图象上,AB∥y轴,与
的图象上,AB∥y轴,与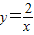 的图象交于点B,AC、BD与x轴平行,分别与
的图象交于点B,AC、BD与x轴平行,分别与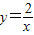 ,
,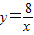 的图象交于点C、D.
的图象交于点C、D.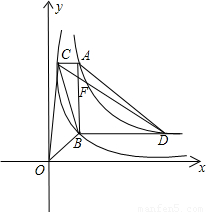
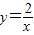 和
和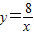 在平面直角坐标系xOy第一象限中的图象如图所示,点A在
在平面直角坐标系xOy第一象限中的图象如图所示,点A在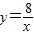 的图象上,AB∥y轴,与
的图象上,AB∥y轴,与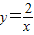 的图象交于点B,AC、BD与x轴平行,分别与
的图象交于点B,AC、BD与x轴平行,分别与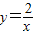 ,
,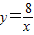 的图象交于点C、D.
的图象交于点C、D.
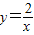 和
和 在平面直角坐标系xOy第一象限中的图象如图所示,点A在
在平面直角坐标系xOy第一象限中的图象如图所示,点A在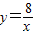 的图象上,AB∥y轴,与
的图象上,AB∥y轴,与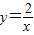 的图象交于点B,AC、BD与x轴平行,分别与
的图象交于点B,AC、BD与x轴平行,分别与 ,
,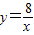 的图象交于点C、D.
的图象交于点C、D.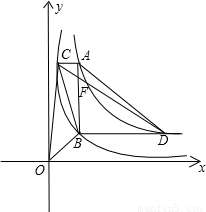
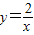 和
和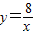 在平面直角坐标系xOy第一象限中的图象如图所示,点A在
在平面直角坐标系xOy第一象限中的图象如图所示,点A在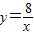 的图象上,AB∥y轴,与
的图象上,AB∥y轴,与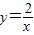 的图象交于点B,AC、BD与x轴平行,分别与
的图象交于点B,AC、BD与x轴平行,分别与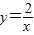 ,
, 的图象交于点C、D.
的图象交于点C、D.