题目内容
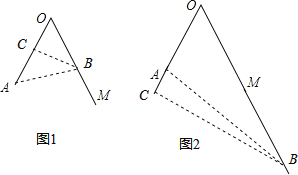
【题目】如图，已知∠AOM=60°，在射线OM上有点B，使得AB与OB的长度都是整数，由此称B是“和谐点”，若OA=8，当B为“和谐点”时，AB和OB的长分别为_____________.
【答案】
或
或
或
．（AB=x,OB=y)
【解析】试题解析：过点B作BC⊥OA，交OA于点C，连接AB，可能有两种情况，垂足在OA上或者垂足在OA延长线上．
设OB=y，AB=x，
∵∠AOM=60°，
∴OC=OBcos60°=
y，
∴AC=OA-OC=8-
y或AC=OC-OA=
y -8，
∵BC2=OB2-OC2，BC2=AB2-AC2，
∴y2-（
y）2=x2-（8-
y）2或x2-（
y -8）2=y2-（
y）2，
∴x2-（y-4）2=48，
∵x与y是正整数，且y必为正整数，x-4为大于等于-4的整数，
将原方程转为 X2-Y2=48，先求（X+Y）（X-Y）=48的正整数解，
∵（X+Y）和（X-Y）同奇同偶，
∴（X+Y）和（X-Y）同为偶数；
∴X2-Y2=48可能有几组正整数解：
， 
， 
，
解得： 
， 
， 
，
∴x的可能值有3个：x=7，x=8或x=13，
当x=7时，y-4=±1，y=3或y=5；
当x=8时，y-4=±4，y=8或y=0（舍去）；
当x=13时，y-4=±11，y=15或y=-7（舍去）；
∴共有4组解： 
或
或
或
．
练习册系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
