Question

如图，上午8时，一艘轮船从A处出发以每小时20海里的速度向正北航行，10时到达B处，则轮船在A处测得灯塔C在北偏西36°，航行到B处时，又测得灯塔C在北偏西72°，求从B到灯塔C的距离。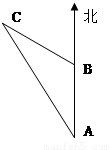

 

Answer 1

【答案】

从B到灯塔C的距离40海里

【解析】

试题分析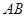：＝20×（10－8）＝40(海里)          

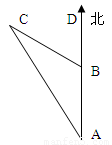
∵∠CBD=72°,∠A=36°

∴∠C=∠CBD-∠A=72°－36°=36°            

∴∠C=∠A=36°

∴BC=AB=40(海里)                

∴从B到灯塔C的距离40海里。

考点：解三角形

点评：本题考查解三角形，本题通过证明三角形是等腰三角形，从而得出本题的解